Question

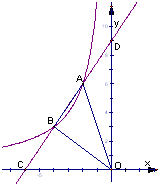
如图，直线AB与x轴交于点C，与反比例函数在第二象限的图象交于点A（-2，6）、点B（-4，m）．
（1）求k，m的值； （2）求直线AB的解析式； （3）求△AOB的面积．

Answer 1

【答案】分析：（1）利用反比例函数图象上点的坐标特征，将点A（-2，6）代入反比例函数解析式求得k值；然后将点B的坐标代入反比例函数解析式，列出关于m的方程，解方程即可；
（2）设直线AB的解析式是y=kx+b，然后利用待定系数法求得直线方程；
（3）过A、B分别作AF⊥y轴于F，BE⊥y轴于E，根据图形计算S_△AOB=S_梯形ABEF+S_△BOE-S_△AOF=S_梯形ABEF即可．
解答：解：（1）∵反比例函数的图象经过点A（-2，6），
k=-2×6=-12…（2分）；
又反比例函数的图象经过点B（-4，m），
∴m=-12÷（-4）=3…（4分）

（2）设直线AB的解析式是y=kx+b，把点A、B坐标分别代入上式得，
，
解得k=，b=9
∴…（8分）

（3）过A、B分别作AF⊥y轴于F，BE⊥y轴于E，
S_△AOB=S_梯形ABEF+S_△BOE-S_△AOF
=S_梯形ABEF
=…（12分）
点评：本题考查了反比例函数综合题．解题时，利用了反比例函数图象上点的坐标特征、待定系数法求反比例函数的解析式．同时要注意运用数形结合的思想．