Question

如图，抛物线y=

1

2

x²+

1

2

x-2，经过点C（-3，h），CD⊥x轴，垂足为D点，Rt△AOB≌Rt△CDA，A、B分别在x轴，y轴上，在对称轴右侧的抛物线上是否存在两点P、Q，使四边形ABPQ是正方形？若存在，求出点P、Q的坐标；若不存在，说请明理由．

Answer 1

分析：将点C（-3，h）代入抛物线y=

1

2

x²+

1

2

x-2，可求点C的坐标，根据全等三角形的性质可得OA=CD=1，OB=AD=3-1=2，以AB为边在抛物线的右侧作正方形AQPB，过P作PE⊥y轴，过Q作QG垂直x轴于G，不难得出三角形ABO和三角形BPE和三角形QAG都全等，据此可求出P，Q的坐标，然后将两点坐标代入抛物线的解析式中即可判断出P、Q是否在抛物线上．

解答：解：在抛物线（对称轴的右侧）上存在点P、Q，使四边形ABPQ是正方形．
把点C（-3，h）代入抛物线y=

1

2

x²+

1

2

x-2，
则h=

1

2

×（-3）²+

1

2

×（-3）-2=1，
则C点坐标为（-3，1），
∵Rt△AOB≌Rt△CDA，
∴OA=CD=1，
∴OB=AD=3-1=2，
以AB为边在AB的右侧作正方形ABPQ，过P作PE⊥OB于E，QG⊥x轴于G，可证△PBE≌△AQG≌△BAO，

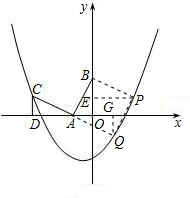
∴PE=AG=BO=2，BE=QG=AO=1，
∴P点坐标为（2，1），Q点坐标为（1，-1）．
y=

1

2

x²+

1

2

x-2，当x=2时，y=1；当x=1时，y=-1．
∴P、Q在抛物线上．
故在抛物线（对称轴的右侧）上存在点P（2，1）、Q（1，-1），使四边形ABPQ是正方形．

点评：本题主要考查了二次函数解析式的应用、正方形的判定、全等三角形的判定和性质等知识点．综合性强，涉及的知识点多，难度较大．