题目内容
有两个角对应相等,并且有一边相等的两个三角形一定全等吗?如果一定全等,请说明理由;如果不一定全等,请举出反例,并且画出图形.
解:一定.
如图:在△ABC和△DEF中,
∠A=∠D,∠B=∠E,若AB=DE,
∴△ABC≌△DEF(ASA);
在△ABC和△DEF中,
∠A=∠D,∠B=∠E,若AC=DF,
∴△ABC≌△DEF(AAS);
在△ABC和△DEF中,
∠A=∠D,∠B=∠E,若BC=EF,
∴△ABC≌△DEF(AAS);
综上,有两个角对应相等,并且有一边相等的两个三角形一定全等.
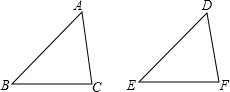
分析:不一定.因为全等三角形的判定定理有(SSS、SAS、ASA、AAS、HL.).AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
点评:本题主要考查了全等三角形判定定理的相关知识,只有熟练掌握这些知识,才能正确解答.
如图:在△ABC和△DEF中,
∠A=∠D,∠B=∠E,若AB=DE,
∴△ABC≌△DEF(ASA);
在△ABC和△DEF中,
∠A=∠D,∠B=∠E,若AC=DF,
∴△ABC≌△DEF(AAS);
在△ABC和△DEF中,
∠A=∠D,∠B=∠E,若BC=EF,
∴△ABC≌△DEF(AAS);
综上,有两个角对应相等,并且有一边相等的两个三角形一定全等.

分析:不一定.因为全等三角形的判定定理有(SSS、SAS、ASA、AAS、HL.).AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
点评:本题主要考查了全等三角形判定定理的相关知识,只有熟练掌握这些知识,才能正确解答.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
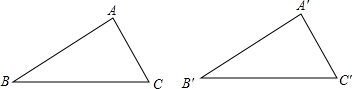
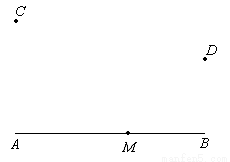
 (2013•河池)请在图中补全坐标系及缺失的部分,并在横线上写恰当的内容.图中各点坐标如下:A(1,0),B(6,0),C(1,3),D(6,2).线段AB上有一点M,使△ACM∽△BDM,且相似比不等于1.求出点M的坐标并证明你的结论.
(2013•河池)请在图中补全坐标系及缺失的部分,并在横线上写恰当的内容.图中各点坐标如下:A(1,0),B(6,0),C(1,3),D(6,2).线段AB上有一点M,使△ACM∽△BDM,且相似比不等于1.求出点M的坐标并证明你的结论.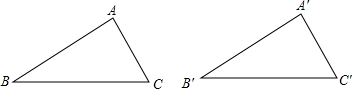
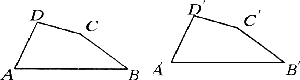
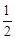 (180°- ) =45°。 ∠BDM=45°(同理)。
(180°- ) =45°。 ∠BDM=45°(同理)。