Question

能够互相重合的多边形叫做全等形，即如果两个多边形对应角相等，对应边相等，那么两个多边形一定全等．但判定两个三角形全等只需三组对应量相等即可，如SAS，SSS等，但如果要判定两个四边形全等仅有四组量对应相等是不够的，必须具备至少五组量对应相等．

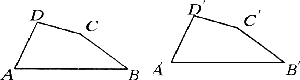
(1)请写出两个四边形全等的一种判定方法(五组量对应相等)；

(2)如图，简要说明你的判定方法是正确的；

(3)举例说明仅有四边对应相等的两个四边形不一定全等(画出图形并简要说明理由)．

Answer 1

答案：
解析：

解：(1)∠D＝∠，AD＝，DC＝，BC＝，AB＝′； 　　(2)连接AC，在△ADC和△中，因为AD＝，∠D＝∠，DC＝，所以△ADC≌△，则AC＝，从而得△ACB≌△，从而得到四边形ABCD和四边形的对应角，对应边均相等，即有四边形ABCD≌四边形； 　　(3)举一个凸四边形和凹四边形．