ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
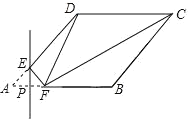
ЃЌ![]() .ЕуPДгЕуAГіЗЂЃЌвдУПУы
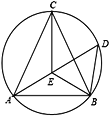
.ЕуPДгЕуAГіЗЂЃЌвдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕуCдЫЖЏ.ЕуQДгЕуBГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕуAдЫЖЏ.СЌНсPQЃЌНЋЯпЖЮPQШЦЕуQЫГЪБеыа§зЊ
ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕуCдЫЖЏ.ЕуQДгЕуBГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕуAдЫЖЏ.СЌНсPQЃЌНЋЯпЖЮPQШЦЕуQЫГЪБеыа§зЊ![]() ЕУЕНЯпЖЮQEЃЌвдPQЁЂQEЮЊБпзїе§ЗНаЮPQEF.ЩшЕуPдЫЖЏЕФЪБМфЮЊtУы
ЕУЕНЯпЖЮQEЃЌвдPQЁЂQEЮЊБпзїе§ЗНаЮPQEF.ЩшЕуPдЫЖЏЕФЪБМфЮЊtУы![]() .
.
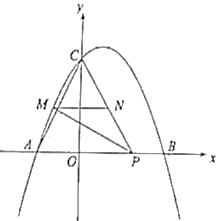
(1).ЕуPЕНБпABЕФОрРыЮЊ______(гУКЌtЕФДњЪ§ЪНБэЪО).
(2).ЕБ![]() ЪБЃЌЧѓtЕФжЕ.
ЪБЃЌЧѓtЕФжЕ.
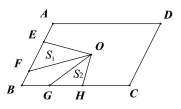
(3).СЌНсBE.Щш![]() ЕФУцЛ§ЮЊSЃЌЧѓSгыtжЎМфЕФКЏЪ§ЙиЯЕЪН.
ЕФУцЛ§ЮЊSЃЌЧѓSгыtжЎМфЕФКЏЪ§ЙиЯЕЪН.
ЁОД№АИЁП(1)tЃЛ(2)t=1ЃЛ(3)![]() (
(![]() )ЃЛ
)ЃЛ![]() (
(![]() )
)
ЁОНтЮіЁП
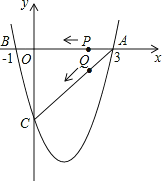
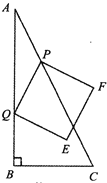
ЃЈ1ЃЉзїPDЁЭABгкDЃЌИљОнЯрЫЦШ§НЧаЮЖдгІБпГЩБШР§ПЩЕУPЕНБпABЕФОрРыЃЛ
ЃЈ2ЃЉИљОнЁїAQPЁзЁїABCЃЌСаБШР§ЪНПЩЕУ![]() ЃЌгЩ
ЃЌгЩ![]() ЃЌ
ЃЌ![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЗжЧщПіЬжТлЃЌЕБ![]() ЪБЃЌЕБ
ЪБЃЌЕБ![]() ЪБЃЌЗжБ№ЧѓГі
ЪБЃЌЗжБ№ЧѓГі![]() ЃЌ
ЃЌ![]() ЃЌСаЪНМЦЫуМДПЩЃЛ
ЃЌСаЪНМЦЫуМДПЩЃЛ
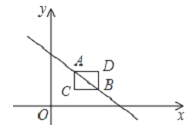
(1)зїPDЁЭABгкDЃЌдђPDЁЮBCЃЌЁрЁїADPЁзЁїABCЃЌЁр![]() ЃЌAP=
ЃЌAP=![]() tЃЌAB=4ЃЌBC=2ЃЌЁр
tЃЌAB=4ЃЌBC=2ЃЌЁр![]() ,ЁрDP=tЃЛ
,ЁрDP=tЃЛ

(2)ШчЭМЂйЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ
Ёп![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁрЁїAQPЁзЁїABCЃЎ
![]() ЃЎ
ЃЎ
Ёп![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ

(3)ЕБ![]() ЪБЃЌШчЭМЂкЃЌ
ЪБЃЌШчЭМЂкЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ
![]() ЃЎ
ЃЎ
ЕБ![]() ЪБЃЌШчЭМЂлЃЌ
ЪБЃЌШчЭМЂлЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ
![]() ЃЎ
ЃЎ



СЗЯАВсЯЕСаД№АИ
 ШЋГЬН№ОэЯЕСаД№АИ
ШЋГЬН№ОэЯЕСаД№АИ
ЯрЙиЬтФП