题目内容
(1)【操作发现】:
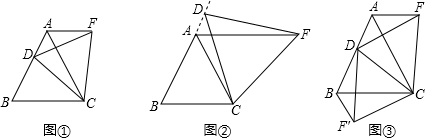
如图①,D是等边△ABC边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF.线段AF与BD之间的数量关系是______.
(2)【类比猜想】:
如图②,当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?并加以证明.
(3)【深入探究】
图③,当动点D在等边△ABC边BA上运动时(点D与点B不重合)连接DC,以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′,连接AF、BF′,探究AF、BF′与AB有何数量关系?并证明你探究的结论.
解:(1)∵△ABC和△DCF都是等边三角形,
∴AC=BC,CD=CF,∠ACB=∠DCF=60°,
∴∠ACB-∠ACD=∠DCF-∠ACD,
即∠BCD=∠ACF,
在△BCD和△ACF中,
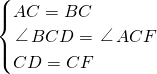 ,
,
∴△BCD≌△ACF(SAS),
∴AF=BD;
(2)结论依然成立.
理由如下:∵△ABC和△DCF都是等边三角形,
∴AC=BC,CD=CF,∠ACB=∠DCF=60°,
∴∠ACB+∠ACD=∠DCF+∠ACD,
即∠BCD=∠ACF,
在△BCD和△ACF中,
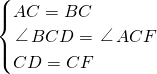 ,
,
∴△BCD≌△ACF(SAS),
∴AF=BD;
(3)AF+BF′=AB.
证明如下:由(1)知,△BCD≌△ACF(SAS),
∴BD=AF,
同理可证,△BCF′≌△DCA(SAS),
∴BF′=AD,
∴AF+BF′=AB.
分析:(1)根据等边三角形的性质可得AC=BC,CD=CF,∠ACB=∠DCF,再求出∠BCD=∠ACF,然后利用“边角边”证明△BCD和△ACF全等,根据全等三角形对应边相等证明即可;
(2)根据等边三角形的性质可得AC=BC,CD=CF,∠ACB=∠DCF,再求出∠BCD=∠ACF,然后利用“边角边”证明△BCD和△ACF全等,根据全等三角形对应边相等证明即可;
(3)同理可证△BCD和△ACF全等,根据全等三角形对应边相等可得BD=AF,△BCF′和△DCA全等,根据全等三角形对应边相等可得BF′=AD,即可得解.
点评:本题考查了全等三角形的判定与性质,等边三角形的性质,熟记等边三角形的性质求出三角形全等的条件是解题的关键.
∴AC=BC,CD=CF,∠ACB=∠DCF=60°,
∴∠ACB-∠ACD=∠DCF-∠ACD,
即∠BCD=∠ACF,
在△BCD和△ACF中,
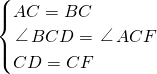 ,
,∴△BCD≌△ACF(SAS),
∴AF=BD;
(2)结论依然成立.
理由如下:∵△ABC和△DCF都是等边三角形,
∴AC=BC,CD=CF,∠ACB=∠DCF=60°,
∴∠ACB+∠ACD=∠DCF+∠ACD,
即∠BCD=∠ACF,
在△BCD和△ACF中,
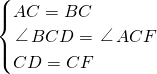 ,
,∴△BCD≌△ACF(SAS),
∴AF=BD;
(3)AF+BF′=AB.
证明如下:由(1)知,△BCD≌△ACF(SAS),
∴BD=AF,
同理可证,△BCF′≌△DCA(SAS),
∴BF′=AD,
∴AF+BF′=AB.
分析:(1)根据等边三角形的性质可得AC=BC,CD=CF,∠ACB=∠DCF,再求出∠BCD=∠ACF,然后利用“边角边”证明△BCD和△ACF全等,根据全等三角形对应边相等证明即可;
(2)根据等边三角形的性质可得AC=BC,CD=CF,∠ACB=∠DCF,再求出∠BCD=∠ACF,然后利用“边角边”证明△BCD和△ACF全等,根据全等三角形对应边相等证明即可;
(3)同理可证△BCD和△ACF全等,根据全等三角形对应边相等可得BD=AF,△BCF′和△DCA全等,根据全等三角形对应边相等可得BF′=AD,即可得解.
点评:本题考查了全等三角形的判定与性质,等边三角形的性质,熟记等边三角形的性质求出三角形全等的条件是解题的关键.

练习册系列答案
相关题目



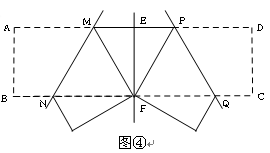
 次旋转和一次平移复制形成一个四
次旋转和一次平移复制形成一个四 边形,在图2的方框内画出草图,并仿照图1作出标记.
边形,在图2的方框内画出草图,并仿照图1作出标记. 处,折痕为EF,若∠ABE=20°,那么
处,折痕为EF,若∠ABE=20°,那么 的度数为 。
的度数为 。