题目内容
 如图,求梯形DBCE的面积.
如图,求梯形DBCE的面积.考点:面积及等积变换
专题:
分析:首先设S△DOE=a,BE与CD交于O,由DE∥BC,可得△ADE∽△ABC,△DOE∽△COB,即可证得AD:AB=OE:OB,然后根据等高三角形的面积比等于对应底的比,可证得S△ADE:S△ABE=S△DOE:S△BOD,则可得方程:
=
,解此方程即可求得△DOE的面积,然后由相似三角形面积比等于相似比的平方,求得△COB的面积,继而求得答案.
| 20 |
| 20+6+a |
| a |
| 6 |
解答: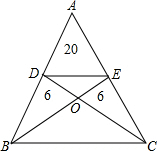 解:设S△DOE=a,BE与CD交于O,
解:设S△DOE=a,BE与CD交于O,
∵DE∥BC,
∴△ADE∽△ABC,△DOE∽△COB,
∴AD:AB=DE:BC,OE:OB=DE:BC,
∴AD:AB=OE:OB,
∵S△ADE:S△ABE=AD:AB,S△DOE:S△BOD=OE:OB,
∴S△ADE:S△ABE=S△DOE:S△BOD,
∴
=
,
∴a2+26a-120=0,
即(a+30)(a-4)=0,
解得:a=4或a=-30(舍去),
∴S△DOE=4,
∴DE:BC=OE:OB=4:6=2:3,
∵
=(
)2=
,
∴S△COB=9,
∴S梯形DBCE=S△DOE+S△BOD+S△COE+S△COB=4+6+6+9=25.
 解:设S△DOE=a,BE与CD交于O,
解:设S△DOE=a,BE与CD交于O,∵DE∥BC,
∴△ADE∽△ABC,△DOE∽△COB,
∴AD:AB=DE:BC,OE:OB=DE:BC,
∴AD:AB=OE:OB,
∵S△ADE:S△ABE=AD:AB,S△DOE:S△BOD=OE:OB,
∴S△ADE:S△ABE=S△DOE:S△BOD,
∴
| 20 |
| 20+6+a |
| a |
| 6 |
∴a2+26a-120=0,
即(a+30)(a-4)=0,
解得:a=4或a=-30(舍去),
∴S△DOE=4,
∴DE:BC=OE:OB=4:6=2:3,
∵
| S△DOE |
| S△COB |
| DE |
| BC |
| 4 |
| 9 |
∴S△COB=9,
∴S梯形DBCE=S△DOE+S△BOD+S△COE+S△COB=4+6+6+9=25.
点评:此题考查了面积与等积变换,涉及了相似三角形的判定与性质以及梯形的性质.此题难度较大,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
下列说法中,错误的是( )
| A、有限小数都是有理数 | ||
| B、无限小数都是无理数 | ||
| C、正数包括正有理数和正无理数,负数包括负有理数和负无理数 | ||
D、
|
