题目内容
 如图,点C在线段AB上,DA⊥AB,EB⊥AB,FC⊥AB,且DA=BC,EB=AC,FC=AB,∠AFB=51°,求∠DFE度数.
如图,点C在线段AB上,DA⊥AB,EB⊥AB,FC⊥AB,且DA=BC,EB=AC,FC=AB,∠AFB=51°,求∠DFE度数.
 证明:如图,连接BD、AE,
证明:如图,连接BD、AE,∵DA⊥AB,FC⊥AB,
∴AD∥CF,∠DAB=∠BCF=90°,
又∵DA=BC,FC=AB,
∴△DAB≌△BCF(SAS),
∴BD=BF,
∴∠BDF=∠BFD,
又∵AD∥CF,
∴∠ADF=∠CFD,
∴∠ABF=∠DFB+∠ADF=∠BFC+2∠CFD,
同理可得,∠BAF=∠AFC+2∠CFE,
又∵∠AFB=51°,
∴∠ABF+∠BAF=129°,
∴∠BFC+2∠CFD+∠AFC+2∠CFE=51°+2∠DFE=129°,
∴∠DFE=39°.
答:∠DFE度数是39°.
分析:如图,连接BD、AE,易证△DAB≌△BCF(SAS),得BD=BF,∠BDF=∠BFD,又∵AD∥CF,∠ADF=∠CFD,所以∠ABF=∠DFB+∠ADF=∠BFC+2∠CFD,同理可得,∠BAF=∠AFC+2∠CFE,又由∠AFB=51°,则∠ABF+∠BAF=129°,所以,∠BFC+2∠CFD+∠AFC+2∠CFE=51°+2∠DFE=129°,解得∠DFE=39°.
点评:本题主要考查了等腰三角形性质和全等三角形的判定与性质,全等三角形的判定是证明线段和角相等的重要方法,作好辅助线是解答本题的关键.

练习册系列答案
相关题目

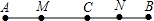
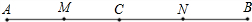
 (1)已知:如图,点C在线段AB上,AC=18cm,BC=6cm,点M、N分别是AC、BC的中点,求MN的长;
(1)已知:如图,点C在线段AB上,AC=18cm,BC=6cm,点M、N分别是AC、BC的中点,求MN的长; 如图,点M在线段AB上,MB=4cm,NB=9cm,且N是AM的中点,则AB=
如图,点M在线段AB上,MB=4cm,NB=9cm,且N是AM的中点,则AB=