题目内容
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在坐标轴上,点B的坐标为(4,2),直线y=﹣ x+3交AB,BC于点M,N,反比例函数y=
x+3交AB,BC于点M,N,反比例函数y= 的图象经过点M,N.
的图象经过点M,N.
(1)求反比例函数的解析式;
(2)若点P在x轴上,且△OPM的面 积与四边形BMON的面积相等,求点P的坐标.
积与四边形BMON的面积相等,求点P的坐标.

解:(1)∵B(4,2),四边形OABC是矩形,
∴OA=BC=2,
将y=2代入y=﹣ x+3得:x=2,
x+3得:x=2,
∴M(2,2),
把M的坐标代入y= 得:k=4,
得:k=4,
∴反比例函数的解析式是y= ;
;
(2)把x=4代入y= 得:y=1,即CN=1,
得:y=1,即CN=1,
∵S四边形BMON=S矩形OABC﹣S△AOM﹣S△CON
=4×2﹣ ×2×2﹣
×2×2﹣ ×4×1=4,
×4×1=4,
由题意得: |OP|×AO=4,
|OP|×AO=4,
∵AO=2,
∴|OP|=4,
∴点P的坐标是(4,0)或(﹣4,0).



练习册系列答案
相关题目
下列运算正确的是( )
|
| A. | a•a2=a2 | B. | (a2)3=a6 | C. | a2+a3=a6 | D. | a6÷a2=a3 |

 ,则
,则 = .
= .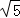 ,则下列结论中正确的是( )
,则下列结论中正确的是( )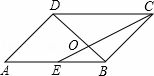
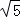 C. m=3
C. m=3 B的长是 .
B的长是 .

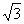 )、B(-1,0),过点A作AB的垂线交
)、B(-1,0),过点A作AB的垂线交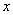 轴于点A1,过点A1作A A1的垂线交
轴于点A1,过点A1作A A1的垂线交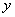 轴于点A2,过点A2作A1A2的垂线交
轴于点A2,过点A2作A1A2的垂线交