题目内容

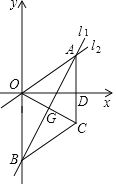
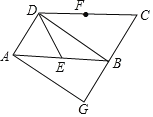
【题目】如图，ABCD中，∠ADC=120°，ADAB，E、F分别是AB、CD的中点，过点A作AG∥BD，交CB的延长线于点G．

（1）求证：DE=BE；

（2）请判断四边形AGBD是什么特殊的四边形，并说明理由．

【答案】（1）证明见解析；（2）四边形AGBD是矩形．理由见解析．

【解析】

（1）先根据平行四边形的性质、平行线的性质可得，再根据线段中点的定义可得，然后根据等边三角形的判定与性质可得，最后根据等量代换即可得证；

（2）先根据平行四边形的判定可知四边形AGBD是平行四边形，再由（1）易知，从而根据矩形的判定即可得出答案．

（1）∵四边形ABCD是平行四边形

∵

E是AB的中点

是等边三角形

；

（2）四边形AGBD是矩形．理由如下：

且

∴四边形AGBD是平行四边形

由（1）的证明知

∴平行四边形AGBD是矩形．

练习册系列答案
相关题目

【题目】已知，在△ABC中，∠BAC=90°，∠ABC=45°，点D为直线BC上一动点（点D不与点B，C重合）．以AD为边做正方形ADEF，连接CF

（1）如图1，当点D在线段BC上时．求证CF+CD=BC；

（2）如图2，当点D在线段BC的延长线上时，其他条件不变，请直接写出CF，BC，CD三条线段之间的关系；

（3）如图3，当点D在线段BC的反向延长线上时，且点A，F分别在直线BC的两侧，其他条件不变；

①请直接写出CF，BC，CD三条线段之间的关系；

②若正方形ADEF的边长为，对角线AE，DF相交于点O，连接OC．求OC的长度．

【题目】如图，在平面直角坐标系中，直线l：yx与直线l：y=kx+b相交于点A（a，3），直线交l交y轴于点B（0，﹣5）．

（1）求直线l的解析式；

（2）将△OAB沿直线l翻折得到△CAB（其中点O的对应点为点C），求证：AC∥OB；

（3）在直线BC下方以BC为边作等腰直角三角形BCP，直接写出点P的坐标．

【题目】如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC．设MN交∠ACB的平分线于点E，交∠ACB的外角平分线于点F．

（1）求证：OE=OF；

（2）若CE=12，CF=5，求OC的长；

（3）当点O在边AC上运动到什么位置时，四边形AECF是矩形？并说明理由．

【题目】已知二次函数y=ax2+bx+c的图象如图所示．下列结论：①abc＞0；②2a﹣b＜0；③4a﹣2b+c＜0；④（a+c）2＜b2其中正确的个数有（ ）

A. 1 B. 2 C. 3 D. 4

【题目】解答下列各题

（1）已知：如图1，直线AB、CD被直线AC所截，点E在AC上，且∠A＝∠D+∠CED，求证：AB∥CD；

（2）如图2，在正方形ABCD中，AB＝8，BE＝6，DF＝4．

①试判断△AEF的形状，并说明理由；

②求△AEF的面积．

【题目】已知：△ABC中，BO平分∠ABC，CO平分∠ACB

（1）如图1，∠BOC和∠A有怎样的数量关系？请说明理由

（2）如图2，过O点的直线分别交△ABC的边AB、AC于E、F（点E不与A，B重合，点F不与A、C重合），BP平分外角∠DBC，CP平分外角∠GCB，BP，CP相交于P．求证：∠P＝∠BOE+∠COF；

（3）如果（2）中过O点的直线与AB交于E（点E不与A、B重合），与CA的延长线交于F在其它条件不变的情况下，请直接写出∠P、∠BOE、∠COF三个角之间的数量关系．

【题目】春节即将来临，根据习俗好多家庭都会在门口挂红灯笼和贴对联．某商店看准了商机，准备购进批红灯笼和对联进行销售，已知红灯笼的进价是对联进价的2.25倍，用720元购进对联的数量比用540元购进红灯笼的数量多60件

（1）对联和红灯笼的进价分别为多少？

（2）由于销售火爆，第一批售完后，该商店以相同的进价再购进300幅对联和200个红灯笼．已知对联的销售价格为12元一幅，红灯笼的销售价格为24元一个．销售一段时间后发现对联售出了总数的，红灯笼售出了总数的．为了清仓，该店老板决定对剩下的红灯笼和对联以相同的折扣数打折销售，并很快全部售出，问商店最低打几折，才能使总的利润率不低于20%？

【题目】已知：如图，，点是的中点，平分，.

（1）求证：；

（2）若，试判断的形状，并说明理由.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网