题目内容
如图，如果抛物线y=ax2+bx+c与x轴交于A、B两点，与y轴交于C点，且OB=OC=
OA，那么b=________．
-
分析：首先设点B的坐标为：（m，0），由OB=OC=OA，即可得A与C的坐标，然后利用待定系数法即可求得b的值．
解答：设点B的坐标为：（m，0），
∵OB=OC=OA，
∴A（-2m，0），C（0，m），
抛物线y=ax2+bx+c与x轴交于A、B两点，与y轴交于C点，
∴
，
解得：b=-．
故答案为：-．
点评：此题考查了待定系数法与方程组的解法．此题难度适中，解题的关键是掌握点与函数的关系．
分析：首先设点B的坐标为：（m，0），由OB=OC=
OA，即可得A与C的坐标，然后利用待定系数法即可求得b的值．解答：设点B的坐标为：（m，0），
∵OB=OC=
OA，∴A（-2m，0），C（0，m），
抛物线y=ax2+bx+c与x轴交于A、B两点，与y轴交于C点，
∴
，解得：b=-
．故答案为：-
．点评：此题考查了待定系数法与方程组的解法．此题难度适中，解题的关键是掌握点与函数的关系．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
某幢建筑物，从10米高的窗口A用水管和向外喷水，喷的水流呈抛物线（抛物线所在平面与墙面垂直），（如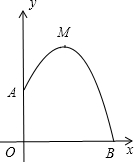
图）如果抛物线的最高点M离墙1米，离地面
米，则水流下落点B离墙距离OB是（ ）
图）如果抛物线的最高点M离墙1米，离地面| 40 |
| 3 |
| A、2米 | B、3米 | C、4米 | D、5米 |
某幢建筑物，从10m高的窗口A，用水管向外喷水，喷出的水流呈抛物线状（抛物线所在的平面与墙面垂直，如图，如果抛物线的最高点M离墙1m，离地面
如图，如果抛物线y=ax2+bx+c与x轴交于A、B两点，与y轴交于C点，且OB=OC=
米，则水流下落点B离墙距离OB是（ ）