Question

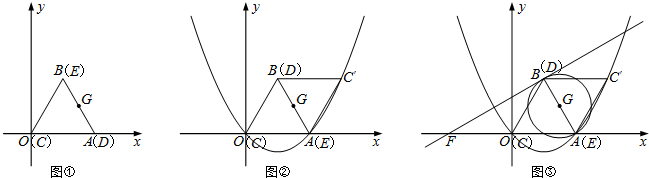
如图①②，在平面直角坐标系中，边长为2的等边△CDE恰好与坐标系中的△OAB重合，现将△CDE绕边AB的中点G（G点也是DE的中点），按顺时针方向旋转180°到△C₁DE的位置．
（1）求C₁点的坐标；
（2）求经过三点O、A、C₁的抛物线的解析式；
（3）如图③，⊙G是以AB为直径的圆，过B点作⊙G的切线与x轴相交于点F，求切线BF的解析式；
（4）抛物线上是否存在一点M，使得S_△AMF：S_△OAB=16：3．若存在，请求出点M的坐标；若不存在，请说明理由．

Answer 1

分析：（1）利用等边三角形的性质，可以求出．
（2）运用待定系数法，代入二次函数解析式，即可求出．
（3）借助切线的性质定理，直角三角形的性质，求出F，B的坐标即可求出解析式．
（4）当M在x轴上方或下方，分两种情况讨论．

解答：解：（1）利用等边三角形的性质可得C₁（3，

3

）；

（2）∵抛物线过原点O（0，0），设抛物线解析式为y=ax²+bx，
把A（2，0），C′（3，

3

）代入，得

4a+2b=0 9a+3b= 3

，
解得a=

3

3

，b=-

2 3

3

，
∴抛物线解析式为y=

3

3

x²-

2 3

3

x；

（3）∵∠ABF=90°，∠BAF=60°，
∴∠AFB=30°，
又∵AB=2，
∴AF=4，
∴OF=2，
∴F（-2，0），
设直线BF的解析式为y=kx+b，
把B（1，

3

），F（-2，0）代入，得

k+b= 3 -2k+b=0

，
解得k=

3

3

，b=

2 3

3

，
∴直线BF的解析式为y=

3

3

x+

2 3

3

；

（4）①当M在x轴上方时，存在M（x，

3

3

x²-

2 3

3

x），
S_△AMF：S_△OAB=[

1

2

×4×（

3

3

x²-

2 3

3

x）]：[

1

2

×2×

3

]=16：3，
得x²-2x-8=0，解得x₁=4，x₂=-2，
当x₁=4时，y=

3

3

×4²-

2 3

3

×4=

8 3

3

，
当x₁=-2时，y=

3

3

×（-2）²-

2 3

3

×（-2）=

8 3

3

，
∴M₁（4，

8 3

3

），M₂（-2，

8 3

3

）；
②当M在x轴下方时，不存在，设点M（x，

3

3

x²-

2 3

3

x），
S_△AMF：S_△OAB=[-

1

2

×4×（

3

3

x²-

2 3

3

x）]：[

1

2

×2×

3

]=16：3，
得x²-2x+8=0，b²-4ac＜0无解，
综上所述，存在点的坐标为M₁（4，

8 3

3

），M₂（-2，

8 3

3

）．

点评：此题主要考查了等边三角形的性质，以及待定系数法求解二次函数解析式和切线的性质定理等，综合性比较强．