题目内容
 如图,反比例函数图象经过点(2,3),且与直线l在第一象限的图象交于A(1,m)、B(3,n)两点.
如图,反比例函数图象经过点(2,3),且与直线l在第一象限的图象交于A(1,m)、B(3,n)两点.
①求这个反比例函数的解析式;
②写出点A、B的坐标,并求直线l的函数解析式.
解:①设反比例函数的解析式为y= ,
,
∵(2,3)在反比例函数的图象上,
∴k=6,
∴反比例函数的解析式y= ;
;
②∵A(1,m)、B(3,n)两点都在反比例函数的图象上,
∴m=6,n=2,
∴A(1,6)、B(3,2),
设直线l的函数解析式y=ax+b,
∴ ,
,
∴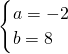 ,
,
∴直线l的函数解析式y=-2x+8.
分析:①设反比例函数的解析式为y= ,将点(2,3)代入反比例函数的解析式,即可得出答案;
,将点(2,3)代入反比例函数的解析式,即可得出答案;
②A(1,m)、B(3,n)两点都在反比例函数的图象上,即可得出k,再设出直线l的函数解析式y=ax+b,将点A、B代入即可得出ab,从而得出直线l的函数解析式.
点评:本题考查了一次函数和反比例函数的交点问题,以及用待定系数法求解析式,是基础知识要熟练掌握.
 ,
,∵(2,3)在反比例函数的图象上,
∴k=6,
∴反比例函数的解析式y=
 ;
;②∵A(1,m)、B(3,n)两点都在反比例函数的图象上,
∴m=6,n=2,
∴A(1,6)、B(3,2),
设直线l的函数解析式y=ax+b,
∴
 ,
,∴
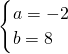 ,
,∴直线l的函数解析式y=-2x+8.
分析:①设反比例函数的解析式为y=
 ,将点(2,3)代入反比例函数的解析式,即可得出答案;
,将点(2,3)代入反比例函数的解析式,即可得出答案;②A(1,m)、B(3,n)两点都在反比例函数的图象上,即可得出k,再设出直线l的函数解析式y=ax+b,将点A、B代入即可得出ab,从而得出直线l的函数解析式.
点评:本题考查了一次函数和反比例函数的交点问题,以及用待定系数法求解析式,是基础知识要熟练掌握.

练习册系列答案
相关题目
 如图,P为反比例函数y=
如图,P为反比例函数y=| k |
| x |
| A、(2,3) |
| B、(-2,6) |
| C、(2,6) |
| D、(-2,3) |
 ,一次函数图象与y轴的交点为C.
,一次函数图象与y轴的交点为C. 如图是反比例函数
如图是反比例函数 如图,反比例函数图象上一点A与坐标轴围成的矩形ABOC的积是8,则该反比例函数的解析式为
如图,反比例函数图象上一点A与坐标轴围成的矩形ABOC的积是8,则该反比例函数的解析式为 如图,反比例函数y=
如图,反比例函数y=