题目内容
3.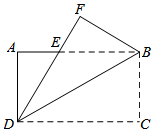 如图,把一张长方形纸片ABCD沿对角线BD对折,使得点C落在点F处,DF交AB于E.如果EF=3,DC=9,那么∠EBF=30°.
如图,把一张长方形纸片ABCD沿对角线BD对折,使得点C落在点F处,DF交AB于E.如果EF=3,DC=9,那么∠EBF=30°.
分析 根据翻折变换的性质得到∠F=∠C=90°,根据全等三角形的判断和性质定理得到BE=6,根据直角三角形的性质解答即可.
解答 解:由翻折变换的性质可知,∠F=∠C=90°,
在△AED和△FEB中,
$\left\{\begin{array}{l}{∠A=∠F}\\{∠AED=∠FEB}\\{AD=FB}\end{array}\right.$,
∴AE=EF=3,又DC=9,
∴BE=6,又∠F=90°,
∴∠EBF=30°,
故答案为:30.
点评 本题考查的是翻折变换的性质,掌握翻折变换是一种对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.

练习册系列答案
相关题目
7.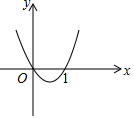 如图为二次函数y=ax2+bx+c的图象,下列各式中:①a>0,②b>0,③c=0,④c=1,⑤a+b+c=0.正确的只有( )
如图为二次函数y=ax2+bx+c的图象,下列各式中:①a>0,②b>0,③c=0,④c=1,⑤a+b+c=0.正确的只有( )
 如图为二次函数y=ax2+bx+c的图象,下列各式中:①a>0,②b>0,③c=0,④c=1,⑤a+b+c=0.正确的只有( )
如图为二次函数y=ax2+bx+c的图象,下列各式中:①a>0,②b>0,③c=0,④c=1,⑤a+b+c=0.正确的只有( )| A. | ①④ | B. | ②③④ | C. | ③④⑤ | D. | ①③⑤ |
15.若m,n都是正整数,且1≤n<m则下列按字母x的降幂排列是( )
| A. | xm+yn-2xy | B. | yn+xm-2xy | C. | xm-2xy+yn | D. | yn-2xy+xm |
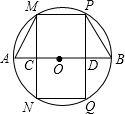 如图,AB是⊙O直径,C、D是AB上两点,MC⊥AB交⊙O于M、N,PD⊥AB交⊙O于P、Q,
如图,AB是⊙O直径,C、D是AB上两点,MC⊥AB交⊙O于M、N,PD⊥AB交⊙O于P、Q,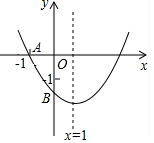 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③4ac-b2<16a;④$\frac{1}{3}$<a<$\frac{2}{3}$;⑤b>c.
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③4ac-b2<16a;④$\frac{1}{3}$<a<$\frac{2}{3}$;⑤b>c.