题目内容
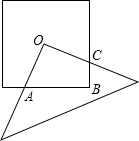 如图,有一块边长为6的正方形,将一块足够大的直角三角板的顶点放在其对角线交点O处,则重叠部分(四边形OABC)的面积为________.
如图,有一块边长为6的正方形,将一块足够大的直角三角板的顶点放在其对角线交点O处,则重叠部分(四边形OABC)的面积为________.
9
分析:连OB、OD,根据正方形的性质得到OA=OB,∠DOB=90°,则∠ODB=∠OBC=45°,而∠AOC=90°,根据等角的余角相等得∠DOA=∠BOC,根据三角形全等的判定方法得到
△ODA≌△OBC,则S△ODA=S△OBC,于是四边形OABC的面积=S△OAB= S正方形=
S正方形= ×62=9.
×62=9.
解答:连OB、OD,如图,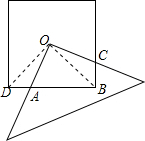
∵点O为正方形的对角线的交点,
∴OA=OB,∠DOB=90°,
∴∠ODB=∠OBC=45°,
∵∠AOC=90°,
∴∠DOA+∠AOB=∠AOB+∠BOC,
∴∠DOA=∠BOC,
在△ODA和△OBC中
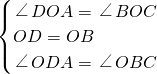 ,
,
∴△ODA≌△OBC,
∴S△ODA=S△OBC,
∴四边形OABC的面积=S△OAB= S正方形=
S正方形= ×62=9.
×62=9.
故答案为9.
点评:本题考查了正方形的性质:正方形四条边都相等,四个角为等于90°;正方形的对角线相等且互相垂直平分.也考查了全等三角形的判定与性质.
分析:连OB、OD,根据正方形的性质得到OA=OB,∠DOB=90°,则∠ODB=∠OBC=45°,而∠AOC=90°,根据等角的余角相等得∠DOA=∠BOC,根据三角形全等的判定方法得到
△ODA≌△OBC,则S△ODA=S△OBC,于是四边形OABC的面积=S△OAB=
 S正方形=
S正方形= ×62=9.
×62=9.解答:连OB、OD,如图,

∵点O为正方形的对角线的交点,
∴OA=OB,∠DOB=90°,
∴∠ODB=∠OBC=45°,
∵∠AOC=90°,
∴∠DOA+∠AOB=∠AOB+∠BOC,
∴∠DOA=∠BOC,
在△ODA和△OBC中
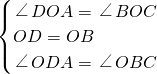 ,
,∴△ODA≌△OBC,
∴S△ODA=S△OBC,
∴四边形OABC的面积=S△OAB=
 S正方形=
S正方形= ×62=9.
×62=9.故答案为9.
点评:本题考查了正方形的性质:正方形四条边都相等,四个角为等于90°;正方形的对角线相等且互相垂直平分.也考查了全等三角形的判定与性质.

练习册系列答案
相关题目
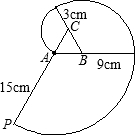 如图,有一块边长为6 cm的正三角形ABC木块,点P是边CA延长线上的一点,在A,P之间拉一细绳,绳长AP为15 cm.握住点P,拉直细绳,把它紧紧缠绕在三角形ABC木块上(缠绕时木块不动),则点P运动的路线长为(精确到0.1厘米,π≈3.14)( )
如图,有一块边长为6 cm的正三角形ABC木块,点P是边CA延长线上的一点,在A,P之间拉一细绳,绳长AP为15 cm.握住点P,拉直细绳,把它紧紧缠绕在三角形ABC木块上(缠绕时木块不动),则点P运动的路线长为(精确到0.1厘米,π≈3.14)( )| A、28.3cm | B、28.2cm | C、56.5cm | D、56.6cm |
 11、如图,有一块边长为4的正方形塑料模板ABCD,将一块足够大的直角三角板的直角顶点落在A点,两条直角边分别与CD交于点F,与CB延长线交于点E.则四边形AECF的面积是
11、如图,有一块边长为4的正方形塑料模板ABCD,将一块足够大的直角三角板的直角顶点落在A点,两条直角边分别与CD交于点F,与CB延长线交于点E.则四边形AECF的面积是
 10、如图,有一块边长为3的正方形塑料模板ABCD,将一块足够大的直角三角板的直角顶点落在A点,两条直角边分别与CD交于点F,与CB延长线交于点E.则四边形AECF的面积是
10、如图,有一块边长为3的正方形塑料模板ABCD,将一块足够大的直角三角板的直角顶点落在A点,两条直角边分别与CD交于点F,与CB延长线交于点E.则四边形AECF的面积是 已知:如图,有一块边长为8m正方形的土地,上面修了横纵各两条路,宽度都是1m,空白部分种上各种花草,求种花草的面积.
已知:如图,有一块边长为8m正方形的土地,上面修了横纵各两条路,宽度都是1m,空白部分种上各种花草,求种花草的面积.