Question

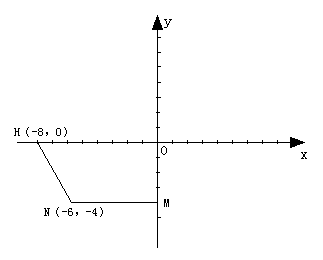
（满分13分）如图11，在平面直角坐标系中，直线与轴、轴分别交于点B、C ；抛物线经过B、C两点，并与轴交于另一点A．

 

（1）求该抛物线所对应的函数关系式；

（2）设是（1）所得抛物线上的一个动点，过点P作直线轴于点M，交直线BC于点N ．

① 若点P在第一象限内．试问：线段PN的长度是否存在最大值 ？若存在，求出它的最大值及此时x的值；若不存在，请说明理由；

② 求以BC为底边的等腰△BPC的面积．

 

Answer 1

 

（1）

（2）①     ② 

解析:（1）由于直线经过B、C两点,令y=0得=3；令=0，得y=3

∴B（3，0），C（0，3）       ……1分

∵点B、C在抛物线上，于是得

                  ……2分

解得b=2，c=3                   ……3分

∴所求函数关系式为  ……4分

（2）①∵点P（,y）在抛物线上，且PN⊥x轴，

∴设点P的坐标为（, ） ……5分

同理可设点N的坐标为（，）     ……6分

又点P在第一象限，

∴PN=PM-NM

=（）-（）

=

=  ……7分

∴当时，

线段PN的长度的最大值为．          ……8分

②解法一：

由题意知，点P在线段BC的垂直平分线上，又由①知，OB=OC

∴BC的中垂线同时也是∠BOC的平分线，

∴设点P的坐标为

又点P在抛物线上,于是有 ∴ …9分

解得          ……10分

∴点P的坐标为： 或  …11分

若点P的坐标为 ，此时点P在第一象限，在Rt△OMP和Rt△BOC中，  ，OB=OC=3

 

 

 

 

若点P的坐标为                          ， 此时点P在第三象限，

则

          ……13分

解法二：由题意知，点P在线段BC的垂直平分线上，

又由①知，OB=OC

∴BC的中垂线同时也是∠BOC的平分线，

∴设点P的坐标为

又点P在抛物线上，于是有

∴    ……9分

解得        ……10分

∴点P的坐标为:

 或 …11分

若点P的坐标为，此时点P在第一象限，在Rt△OMP和Rt△BOC中，

 ，OB=OC=3

若点P的坐标为    ，   此时点P在第三象限，（与解法一相同）……13分

当点P在第一象限时，△BPC面积其它解法有：

①，BC=

②

       

         （本答案仅供参考）