题目内容
如图所示,△ABC是⊙O的内接三角形,AD⊥BC于D点,且AC=5,DC=3,AB= ,则⊙O的直径等于 .
,则⊙O的直径等于 .
【答案】分析:连接AO并延长到E,连接BE.设AE=2R,则∠ABE=90°,∠AEB=∠ACB,∠ADC=90°,利用勾股定理求得AD= =
= =4;再证明Rt△ABE∽Rt△ADC,得到
=4;再证明Rt△ABE∽Rt△ADC,得到 =
= ,即2R=
,即2R= =
= =5
=5 .
.
解答: 解:如图,
解:如图,
连接AO并延长到E,连接BE.设AE=2R,则
∠ABE=90°,∠AEB=∠ACB;
∵AD⊥BC于D点,AC=5,DC=3,AB= ,
,
∴∠ADC=90°,AD= =
= =4;
=4;
在Rt△ABE与Rt△ADC中,
∠ABE=∠ADC=90°,∠AEB=∠ACB,
∴Rt△ABE∽Rt△ADC,
∴ =
= ,
,
即2R= =
= =5
=5 ;
;
∴⊙O的直径等于 .
.
点评:此题比较复杂,解答此题的关键是连接AO并延长到E.连接BE,作出⊙O的直径,再利用三角形相似解答.
 =
= =4;再证明Rt△ABE∽Rt△ADC,得到
=4;再证明Rt△ABE∽Rt△ADC,得到 =
= ,即2R=
,即2R= =
= =5
=5 .
.解答:
 解:如图,
解:如图,连接AO并延长到E,连接BE.设AE=2R,则
∠ABE=90°,∠AEB=∠ACB;
∵AD⊥BC于D点,AC=5,DC=3,AB=
 ,
,∴∠ADC=90°,AD=
 =
= =4;
=4;在Rt△ABE与Rt△ADC中,
∠ABE=∠ADC=90°,∠AEB=∠ACB,
∴Rt△ABE∽Rt△ADC,
∴
 =
= ,
,即2R=
 =
= =5
=5 ;
;∴⊙O的直径等于
 .
.点评:此题比较复杂,解答此题的关键是连接AO并延长到E.连接BE,作出⊙O的直径,再利用三角形相似解答.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
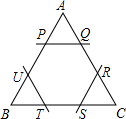 如图所示,△ABC是边长为a的正三角形纸张,今在各角剪去一个三角形,使得剩下的六边形PQRSTU为正六边形,则此正六边形的周长为何( )
如图所示,△ABC是边长为a的正三角形纸张,今在各角剪去一个三角形,使得剩下的六边形PQRSTU为正六边形,则此正六边形的周长为何( )| A、2a | ||
| B、3a | ||
C、
| ||
D、
|
 22、如图所示,△ABC是等边三角形,延长BC至E,延长BA至F,使AF=BE,连接CF、EF,过点F作直线FD⊥CE于D,试发现∠FCE与∠FEC的数量关系,并说明理由.
22、如图所示,△ABC是等边三角形,延长BC至E,延长BA至F,使AF=BE,连接CF、EF,过点F作直线FD⊥CE于D,试发现∠FCE与∠FEC的数量关系,并说明理由. 7、如图所示,△ABC是正三角形,△A1B1 C1的三条边A1B1、BlC1、C1A1交△ABC各边分别于C2、C3,A2、A3,B2、B3.已知A2C3=C2B3=B2A3,且C2C32+B2B32=A2A32.请你证明:AlB1⊥C1A1.
7、如图所示,△ABC是正三角形,△A1B1 C1的三条边A1B1、BlC1、C1A1交△ABC各边分别于C2、C3,A2、A3,B2、B3.已知A2C3=C2B3=B2A3,且C2C32+B2B32=A2A32.请你证明:AlB1⊥C1A1. 12、如图所示,△ABC是等边三角形,AQ=PQ,PR⊥AB于R点,PS⊥AC于S点,PR=PS,则四个结论:①点P在∠A的平分线上;②AS=AR;③QP∥AR;④△BRP≌△QSP,正确的结论是( )
12、如图所示,△ABC是等边三角形,AQ=PQ,PR⊥AB于R点,PS⊥AC于S点,PR=PS,则四个结论:①点P在∠A的平分线上;②AS=AR;③QP∥AR;④△BRP≌△QSP,正确的结论是( ) (2012•黄陂区模拟)如图所示,△ABC是⊙O的内接正三角形,四边形DEFG是⊙O的内接正方形,EF∥BC,则∠AOF为( )
(2012•黄陂区模拟)如图所示,△ABC是⊙O的内接正三角形,四边形DEFG是⊙O的内接正方形,EF∥BC,则∠AOF为( )