题目内容
.(本题15分)马田同学将一张圆桌紧靠在矩形屋子的一角,与相邻两面墙相切,她把切点记为A、B,然后,她又在桌子边缘上任取一点P(异于A、B),通过计算∠APB的度数,她惊奇的发现∠APB的度数的
 ,正好都和她今天作业中的一条抛物线与x轴的交点的横坐标完全相同,她作业中的那条抛物线还经过点C(10,17).聪明的你:
,正好都和她今天作业中的一条抛物线与x轴的交点的横坐标完全相同,她作业中的那条抛物线还经过点C(10,17).聪明的你: (1)请你求出∠APB的度数
(1)请你求出∠APB的度数 (2)请你求出马田同学作业中的
那条抛物线的对称轴方程.
解:(1)设圆桌所在圆的圆心为O,过切点的
 切线AC、BC交于C,p为异于A、B的圆周上的任意一点.
切线AC、BC交于C,p为异于A、B的圆周上的任意一点. 当p在 上时,如图中的p1,连接AP1、BP1、
当p在 上时,如图中的p1,连接AP1、BP1、AO、BO,则OA⊥AC,OB⊥BC,BC⊥AC.
所以,四边形ACBO是矩形,所以,∠AOB=900,
 所以, ∠AP1B=450……………………….4’
所以, ∠AP1B=450……………………….4’当p在 上时,如图中的p2,连接AP2、BP2,
则∠AP2B=1800-450=1350………………………7’
(2)∵∠APB=450或1350
∴
 ………………………8’
………………………8’依题意,9、27是所求抛物线与x轴交点的横坐标,故可设所求的
抛物线的解析式为:y="a(x-9)(x-27)" (a≠0)……………………10’
∵抛物线经过点C(10,17)
∴a(10-9)(10-27)=17
解之得:a=-1…………………………………………………12’
∴y=-(x-9)(x-27)即y=-x2+36x-243 ……………14’
∴抛物线的对称轴方程为x=-
 即x=18…………15解析:
即x=18…………15解析:p;【解析】略

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 (1)请你求出∠APB的度数
(1)请你求出∠APB的度数  ,正好都和她今天作业中的一条抛物线与x轴的交点的横坐标完全相同,她作业中的那条抛物线还经过点C(10,17).聪明的你:
,正好都和她今天作业中的一条抛物线与x轴的交点的横坐标完全相同,她作业中的那条抛物线还经过点C(10,17).聪明的你: (1)请你求出∠APB的度数
(1)请你求出∠APB的度数  ,正好都和她今天作业中的一条抛物线与x轴的交点的横坐标完全相同,她作业中的那条抛物线还经过点C(10,17).聪明的你:
,正好都和她今天作业中的一条抛物线与x轴的交点的横坐标完全相同,她作业中的那条抛物线还经过点C(10,17).聪明的你: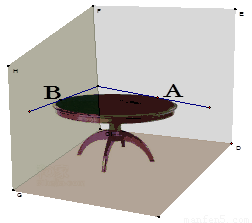 (1)请你求出∠APB的度数
(1)请你求出∠APB的度数