题目内容
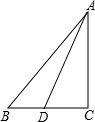
如图,在△ABC中,AD=15,AC=12,DC=9,点B是CD延长线上一点,连接AB,若AB=20.求:△AB D的面积.
D的面积.
【考点】勾股定理;勾股定理的逆定理.
【分析】由勾股定理的逆定理证明△ADC是直角三角形,∠C=90°,再由勾股定理求出BC,得出BD,即可得出结果.
【解答】解:在△ADC中,AD=15,AC=12,DC =9,
=9,
AC2+DC2=122+92=152=AD2,
即AC2+DC2=AD2,
∴△ADC是直角三角形,∠C=90°,
在Rt△ABC中,BC= =
= =16,
=16,
∴BD=BC﹣DC=16﹣9=7,
∴△ABD的面积= ×7×12=42.
×7×12=42.
【点评】本题考查了勾股定理、勾股定理的逆定理;熟练掌握勾股定理,由勾股定理的逆定理证明三角形是直角三角形是解决问题的关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
 端点),请你根据统计图解决下列问题:
端点),请你根据统计图解决下列问题:


 C落在BD上,若∠B=∠D=36°,则∠CAD+∠ACE+∠E=__________°.
C落在BD上,若∠B=∠D=36°,则∠CAD+∠ACE+∠E=__________°.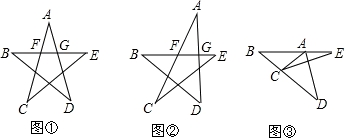
 的相反数是 ,绝对值是
的相反数是 ,绝对值是