题目内容
【题目】如图，等腰△ABC内接于⊙O，已知AB=AC，∠ABC=30°，BD是⊙O的直径，如果CD= 
，则AD= ． 
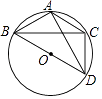
【答案】4
【解析】解：∵AB=AC， ∴∠ABC=∠ACB=∠ADB=30°，
∵BD是直径，
∴∠BAD=90°，∠ABD=60°，
∴∠CBD=∠ABD﹣∠ABC=30°，
∴∠ABC=∠CBD，
∴ 
= 
= 
，
∴ 
= 
，
∴AD=CB，
∵∠BCD=90°，
∴BC=CDtan60°= 
=4，
∴AD=BC=4．
所以答案是4．
【考点精析】利用等腰三角形的性质和含30度角的直角三角形对题目进行判断即可得到答案，需要熟知等腰三角形的两个底角相等（简称：等边对等角）；在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．
练习册系列答案
相关题目
【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况，他从中随机调查了50户居民的月均用水量(单位：t)，并绘制了样本的频数分布表和频数分布直方图(如图)．
(1)请根据题中已有的信息补全频数分布表和频数分布直方图；
月均用水量/t | 频数 | 百分比 |
2≤x＜3 | 2 | 4% |
3≤x＜4 | 12 | 24% |
4≤x＜5 | ||
5≤x＜6 | 10 | 20% |
6≤x＜7 | 12% | |
7≤x＜8 | 3 | 6% |
8≤x＜9 | 2 | 4% |
(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭，请你通过样本估计总体中的中等用水量家庭大约有多少户．
