��Ŀ����
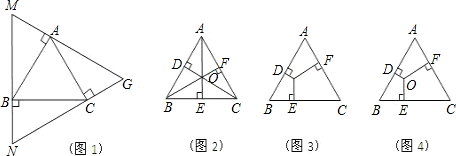
��֪���ȱߡ�ABC�ı߳�Ϊa��̽����1������ͼ1�����ȱߡ�ABC�Ķ���A��B��C������AB��BC��CA�Ĵ���Χ�ɡ�MNG����֤����MNG�ǵȱ���������MN=
 a��
a��̽����2�����ڵȱߡ�ABC��ȡһ��O������O�ֱ���OD��AB��OE��BC��OF��CA������ֱ�Ϊ��D��E��F��
����ͼ2������O�ǡ�ABC�����ģ����ǿ����������������ʽ���ȱ����������ʵõ�������ȷ���ۣ�����֤����������1�� OD+OE+OF=
 a������2�� AD+BE+CF=
a������2�� AD+BE+CF= a��
a������ͼ3������O�ǵȱߡ�ABC������һ�㣬����������1��2�Ƿ���Ȼ��������������������֤�����������������˵�����ɣ�

���𰸡���������1�������С�ABCΪ�ȱ������Σ�AB=BC=a����ABC=60°�������N����G��ֵ����ֱ�ǡ�AMB����CNB�У���������a��ʾ��MB��NBȻ���ٱ�ʾ��MN����������֤��MN= a��
a��
��2���ж����Ƿ������ͨ������ֱ�������Σ���������߶ζ�ת����ֱ���������н�����⣻
�жϢ��Ƿ������ҲҪͨ������ֱ�������Σ��ɸ��ݹ��ɶ�������������߶ζ���ʾ������Ȼ������ó����ۢ��Ƿ���ȷ��
�����1��֤������ͼ1���ߡ�ABCΪ�ȱ������Σ�
���ABC=60°��
��BC��MN��BA��MG��
���CBM=��BAM=90°��
���ABM=90°-��ABC=30°��
���M=90°-��ABM=60°��
ͬ������N=��G=60°��
���MNGΪ�ȱ������Σ�
��Rt��ABM��BM= a��
a��
��Rt��BCN��BN= a��
a��
��MN=BM+BN= a��
a��
��2���ڣ�����1������
֤������ͼ3������O��GH��BC���ֱ�AB��AC�ڵ�G��H������H��HM��BC�ڵ�M��
���DGO=��B=60°����OHF=��C=60°��
���AGH�ǵȱ������Σ�
��GH=AH��
��OE��BC��
��OE��HM��
���ı���OEMH�Ǿ��Σ�
��HM=OE��
��Rt��ODG�У�OD=OG•sin��DGO=OG•sin60°= OG��
OG��
��Rt��OFH�У�OF=OH•sin��OHF=OH•sin60°= OH��
OH��
��Rt��HMC�У�HM=HC•sinC=HC•sin60°= HC��
HC��
��OD+OE+OF=OD+HM+OF= OG+
OG+ HC+
HC+ OH
OH
= ��GH+HC��=
��GH+HC��= AC=
AC= a��
a��
��2���ڣ�����2������
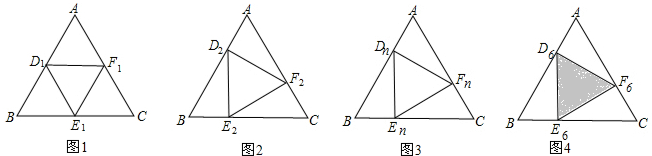
֤������ͼ4������OA��OB��OC�����ݹ��ɶ����ã�
BE2+OE2=OB2=BD2+OD2�٣�
CF2+OF2=OC2=CE2+OE2�ڣ�
AD2+OD2=AO2=AF2+OF2�ۣ�
��+��+�۵ã�BE2+CF2+AD2=BD2+CE2+AF2��
��BE2+CF2+AD2=��a-AD��2+��a-BE��2+��a-CF��2=a2-2AD•a+AD2+a2-2BE•a+BE2+a2-2CF•a+CF2
�����ã�2a��AD+BE+CF��=3a2
��AD+BE+CF= a��
a��
�������������ۺϿ����˵ȱ������ε��ж������ʣ���ֱ�������ε�֪ʶ�㣬����֪ʶ��Ƚ϶࣬������ѶȱȽϴ�
 a��
a����2���ж����Ƿ������ͨ������ֱ�������Σ���������߶ζ�ת����ֱ���������н�����⣻
�жϢ��Ƿ������ҲҪͨ������ֱ�������Σ��ɸ��ݹ��ɶ�������������߶ζ���ʾ������Ȼ������ó����ۢ��Ƿ���ȷ��
�����1��֤������ͼ1���ߡ�ABCΪ�ȱ������Σ�
���ABC=60°��
��BC��MN��BA��MG��
���CBM=��BAM=90°��
���ABM=90°-��ABC=30°��
���M=90°-��ABM=60°��
ͬ������N=��G=60°��
���MNGΪ�ȱ������Σ�
��Rt��ABM��BM=
 a��
a����Rt��BCN��BN=
 a��
a����MN=BM+BN=
 a��
a����2���ڣ�����1������
֤������ͼ3������O��GH��BC���ֱ�AB��AC�ڵ�G��H������H��HM��BC�ڵ�M��
���DGO=��B=60°����OHF=��C=60°��
���AGH�ǵȱ������Σ�
��GH=AH��
��OE��BC��
��OE��HM��

���ı���OEMH�Ǿ��Σ�
��HM=OE��
��Rt��ODG�У�OD=OG•sin��DGO=OG•sin60°=
 OG��
OG����Rt��OFH�У�OF=OH•sin��OHF=OH•sin60°=
 OH��
OH����Rt��HMC�У�HM=HC•sinC=HC•sin60°=
 HC��
HC����OD+OE+OF=OD+HM+OF=
 OG+
OG+ HC+
HC+ OH
OH=
 ��GH+HC��=
��GH+HC��= AC=
AC= a��
a����2���ڣ�����2������

֤������ͼ4������OA��OB��OC�����ݹ��ɶ����ã�
BE2+OE2=OB2=BD2+OD2�٣�
CF2+OF2=OC2=CE2+OE2�ڣ�
AD2+OD2=AO2=AF2+OF2�ۣ�
��+��+�۵ã�BE2+CF2+AD2=BD2+CE2+AF2��
��BE2+CF2+AD2=��a-AD��2+��a-BE��2+��a-CF��2=a2-2AD•a+AD2+a2-2BE•a+BE2+a2-2CF•a+CF2
�����ã�2a��AD+BE+CF��=3a2
��AD+BE+CF=
 a��
a���������������ۺϿ����˵ȱ������ε��ж������ʣ���ֱ�������ε�֪ʶ�㣬����֪ʶ��Ƚ϶࣬������ѶȱȽϴ�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ

 a��
a�� a������2�� AD+BE+CF=
a������2�� AD+BE+CF= a��
a��