题目内容
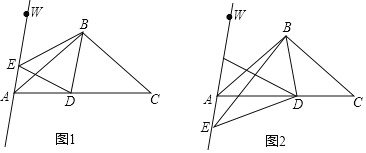
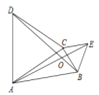
【题目】如图所示,在△ABC中,∠ABC=45°.点D在AB上,点E在BC上,且AE⊥CD,若AE=CD,BE:CE=5:6,S△BDE=75,则S△ABC=_____.

【答案】440.
【解析】
作DM⊥BC于M,AN⊥BC于N,利用AAS证出△AEN≌△CDM,从而得出AN=CM,EN=DM,设BE=5a,用含a的式子分别表示各个线段的长度,根据三角形的面积公式即可求出a2,然后根据三角形的面积公式求面积即可.
解:作DM⊥BC于M,AN⊥BC于N,如图所示:

则∠CMD=∠BMD=∠ANE=90°,
∵∠ABC=45°,
∴△BDM、△BAN是等腰直角三角形,
∴BM=DM,BN=AN,
∵AE⊥CD,
∴∠AEN+∠EAN=∠AEN+∠DCM=90°,
∴∠EAN=∠DCM,
在△AEN和△CDM中,
 ,
,
∴△AEN≌△CDM(AAS),
∴AN=CM,EN=DM,
∴BN=CM,
∴BM=CN,
∴BM=DM=CN=EN,
∵BE:CE=5:6,
∴设BE=5a,
则CE=6a,BC=BE+CE=11a,BM=DM=CN=EN=![]() CE=3a,AN=CM=BC﹣BM=8a,
CE=3a,AN=CM=BC﹣BM=8a,
∴CD2=DM2+CM2=(3a)2+(8a)2=73a2,
∵S△BDE=![]() BE×DM=
BE×DM=![]() ×5a×3a=75,
×5a×3a=75,
∴a2=10,
∴S△ABC=![]() BC×AN=
BC×AN=![]() ×11a ×8a=44 a2=440;
×11a ×8a=44 a2=440;
故答案为:440.

练习册系列答案
相关题目