题目内容
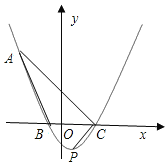
【题目】如图,已知二次函数![]() 的图象经过点A(-3,6),并与x轴交于点B(-1,0)和点C,顶点为点P.
的图象经过点A(-3,6),并与x轴交于点B(-1,0)和点C,顶点为点P.
(1)求这个二次函数解析式;
(2)设D为x轴上一点,满足∠DPC=∠BAC,求点D的坐标;
(3)作直线AP,在抛物线的对称轴上是否存在一点M,在直线AP上是否存在点N,使AM+MN的值最小?若存在,求出M、N的坐标:若不存在,请说明理由.
【答案】(1)点C坐标为(3,0),点P(1,-2);(2)点P(7,0);(3)点N(-![]() ,
,![]() ).
).
【解析】
(1)将点A、B坐标代入二次函数表达式,即可求解;
(2)利用S△ABC= ![]() ×AC×BH=
×AC×BH= ![]() ×BC×yA,求出sinα=
×BC×yA,求出sinα= ![]() ,则tanα=
,则tanα= ![]() ,在△PMD中,tanα=
,在△PMD中,tanα= ![]() =
= ![]() ,即可求解;
,即可求解;
(3)作点A关于对称轴的对称点A′(5,6),过点A′作A′N⊥AP分别交对称轴与点M、交AP于点N,此时AM+MN最小,即可求解.
(1)将点A、B坐标代入二次函数表达式得: ,解得:
,解得: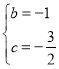 ,
,
故:抛物线的表达式为:y=![]() x2-x-
x2-x-![]() ,
,
令y=0,则x=-1或3,令x=0,则y=-![]() ,
,
故点C坐标为(3,0),点P(1,-2);
(2)过点B作BH⊥AC交于点H,过点P作PG⊥x轴交于点G,

设:∠DPC=∠BAC=α,
由题意得:AB=2![]() ,AC=6
,AC=6![]() ,BC=4,PC=2
,BC=4,PC=2![]() ,
,
S△ABC=![]() ×AC×BH=
×AC×BH=![]() ×BC×yA,
×BC×yA,
解得:BH=2![]() ,
,
sinα=![]() =
=![]() =
=![]() ,则tanα=
,则tanα=![]() ,
,
由题意得:GC=2=PG,故∠PCB=45°,
延长PC,过点D作DM⊥PC交于点M,
则MD=MC=x,
在△PMD中,tanα=![]() =
=![]() =
=![]() ,
,
解得:x=2![]() ,则CD=
,则CD=![]() x=4,
x=4,
故点P(7,0);
(3)作点A关于对称轴的对称点A′(5,6),
过点A′作A′N⊥AP分别交对称轴与点M、交AP于点N,此时AM+MN最小,

直线AP表达式中的k值为:![]() =-2,则直线A′N表达式中的k值为
=-2,则直线A′N表达式中的k值为![]() ,
,
设直线A′N的表达式为:y=![]() x+b,
x+b,
将点A′坐标代入上式并求解得:b=![]() ,
,
故直线A′N的表达式为:y=![]() x+
x+![]() …①,
…①,
当x=1时,y=4,
故点M(1,4),
同理直线AP的表达式为:y=-2x…②,
联立①②两个方程并求解得:x=-![]() ,
,
故点N(-![]() ,
,![]() ).
).

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案