题目内容
9.若抛物线y=x2-2x-3与x轴分别交于A,B两点,则A,B的坐标为(-1,0),(3,0).分析 根据抛物线与x轴的交点问题,通过解方程x2-2x-3=0可得到A、B的坐标.
解答 解:当y=0时,x2-2x-3=0,解得x1=-1,x2=3,
所以抛物线y=x2-2x-3与x轴的两点坐标为(-1,0),(3,0),
即A,B的坐标为(-1,0),(3,0).
故答案为(-1,0),(3,0).
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.

练习册系列答案
相关题目
19.下列给出的x的值,是方程x-6=2x+5的解的是( )
| A. | $x=-\frac{1}{3}$ | B. | x=-1 | C. | x=-11 | D. | $x=\frac{11}{3}$ |
19.阿里巴巴数据显示,2016年天猫商城“双11”全球狂欢交易额超1017亿元,数据1017亿元用科学记数法表示为( )
| A. | 1017×108 | B. | 10.17×1010 | C. | 1.017×1011 | D. | 1.017×1010 |
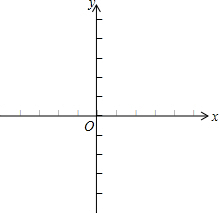 使用五点法画出二次函数y=x2-2x-3的图象.
使用五点法画出二次函数y=x2-2x-3的图象.
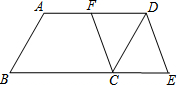 如图,在?ABCD中,F是AD的中点,延长BC到点E,使CE=$\frac{1}{2}$BC,连接DE,CF.
如图,在?ABCD中,F是AD的中点,延长BC到点E,使CE=$\frac{1}{2}$BC,连接DE,CF. 如图,AB=DE,BC=EF,CD=FA,∠A=∠D,求证:∠ABC=∠DEF.
如图,AB=DE,BC=EF,CD=FA,∠A=∠D,求证:∠ABC=∠DEF.