题目内容
 如图,点P是直线
如图,点P是直线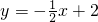 上一动点,当线段OP最短时,OP的长为
上一动点,当线段OP最短时,OP的长为
- A.2
- B.

- C.

- D.

C
分析:根据直线解析式求出点A、B的坐标,再根据勾股定理求出AB的长度,根据点到直线的所有线中,垂线段最短,利用三角形的面积列式即可求解.
解答: 解:当x=0时,y=2,
解:当x=0时,y=2,
当y=0时,- x+2=0,解得x=4,
x+2=0,解得x=4,
∴点A、B的坐标是A(0,2),B(4,0),
∴AB= =2
=2 ,
,
根据垂线段最短的性质,OP⊥AB时,OP最短,
此时,S△AOB= ×OA×OB=
×OA×OB= ×AB×OP,
×AB×OP,
即 ×2×4=
×2×4= ×2
×2 ×OP,
×OP,
解得OP= .
.
故选C.
点评:本题综合考查了一次函数的问题,主要利用勾股定理,垂线段最短的性质,根据直线解析式求出点A、B的坐标是解题的关键.
分析:根据直线解析式求出点A、B的坐标,再根据勾股定理求出AB的长度,根据点到直线的所有线中,垂线段最短,利用三角形的面积列式即可求解.
解答:
 解:当x=0时,y=2,
解:当x=0时,y=2,当y=0时,-
 x+2=0,解得x=4,
x+2=0,解得x=4,∴点A、B的坐标是A(0,2),B(4,0),
∴AB=
 =2
=2 ,
,根据垂线段最短的性质,OP⊥AB时,OP最短,
此时,S△AOB=
 ×OA×OB=
×OA×OB= ×AB×OP,
×AB×OP,即
 ×2×4=
×2×4= ×2
×2 ×OP,
×OP,解得OP=
 .
.故选C.
点评:本题综合考查了一次函数的问题,主要利用勾股定理,垂线段最短的性质,根据直线解析式求出点A、B的坐标是解题的关键.

练习册系列答案
相关题目

 如图,点O是直线AB上的一点,OC是任意一条射线,OD平分∠BOC,OE平分∠AOC.
如图,点O是直线AB上的一点,OC是任意一条射线,OD平分∠BOC,OE平分∠AOC. ,求A,B两点的坐标;
,求A,B两点的坐标;
 :
: 上的点,过点P的另一条直线
上的点,过点P的另一条直线 交抛物线
交抛物线 于A、B两点.
于A、B两点.
 ,求A、B两点的坐标;
,求A、B两点的坐标;  ),当PA=AB时,请直接写出点A的坐标;
),当PA=AB时,请直接写出点A的坐标; 轴于点C,若△AOB的外心在边AB上,且∠BPC=∠OCP,求点P的坐标.
轴于点C,若△AOB的外心在边AB上,且∠BPC=∠OCP,求点P的坐标.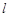 :
: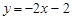 上的点,过点P的另一条直线
上的点,过点P的另一条直线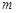 交抛物线
交抛物线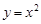 于A、B两点.
于A、B两点.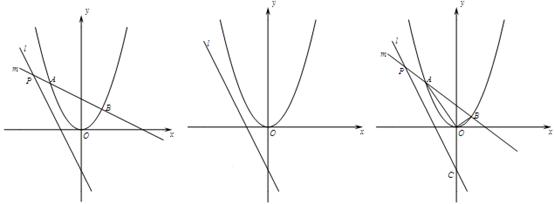
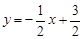 ,求A、B两点的坐标;
,求A、B两点的坐标; 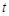 ),当PA=AB时,请直接写出点A的坐标;
),当PA=AB时,请直接写出点A的坐标; 轴于点C,若△AOB的外心在边AB上,且∠BPC=∠OCP,求点P的坐标.
轴于点C,若△AOB的外心在边AB上,且∠BPC=∠OCP,求点P的坐标.