题目内容
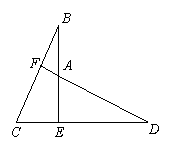
已知：BE⊥CD，BE＝DE，BC＝DA，
求证：① △BEC≌△DAE；
②DF⊥BC．
 |
证明：①∵ＢＥ⊥ＣＤ
∴∠ＢＥＣ＝∠ＤＥＡ＝９０°
在Ｒｔ△ＢＥＣ与Ｒｔ△ＤＥＡ中
ＢＣ＝ＤＡ
ＢＥ＝ＤＥ
∴Ｒｔ△ＢＥＣ≌Ｒｔ△ＤＥＡ（ＨＬ）
②∵Ｒｔ△ＢＥＣ≌Ｒｔ△ＤＥＡ
∴∠Ｃ＝∠ＤＡＥ
∵∠ＤＥＡ＝９０°
∴∠Ｄ＋∠ＤＡＥ＝９０°
∴∠Ｄ＋∠Ｃ＝９０°
∴∠ＤＦＣ＝９０°
∴ＤＦ⊥ＢC
练习册系列答案
相关题目
题目内容
已知：BE⊥CD，BE＝DE，BC＝DA，
求证：① △BEC≌△DAE；
②DF⊥BC．
|
证明：①∵ＢＥ⊥ＣＤ
∴∠ＢＥＣ＝∠ＤＥＡ＝９０°
在Ｒｔ△ＢＥＣ与Ｒｔ△ＤＥＡ中
ＢＣ＝ＤＡ
ＢＥ＝ＤＥ
∴Ｒｔ△ＢＥＣ≌Ｒｔ△ＤＥＡ（ＨＬ）
②∵Ｒｔ△ＢＥＣ≌Ｒｔ△ＤＥＡ
∴∠Ｃ＝∠ＤＡＥ
∵∠ＤＥＡ＝９０°
∴∠Ｄ＋∠ＤＡＥ＝９０°
∴∠Ｄ＋∠Ｃ＝９０°
∴∠ＤＦＣ＝９０°
∴ＤＦ⊥ＢC
有一个动点P, PH⊥OA,垂足为H, △PHO的中线PM与NH交于点G．
；
, 
,求
关于
，则斜边的长为（ ）．
D.