题目内容
在边长为4的正方形ABCD中,E是AD中点,F为DC上一点,且DF= DC,猜想BE与EF的关系?并说明理由.
DC,猜想BE与EF的关系?并说明理由.
解:猜想:BE⊥EF且BE=2EF,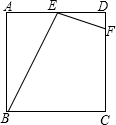 理由如下:
理由如下:
∵四边形ABCD是正方形,
∴∠A=90°,
∵E是AD的中点,
∴AE= AD=
AD= ×4=2,
×4=2,
∴由勾股定理得:BE=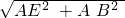 =2
=2 ,
,
同理在直角三角形DEF中,DE=2,DF=1,EF= ,
,
∵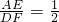 ,
,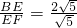 =
= ,
,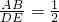 ,
,
∴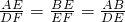 ,
,
∴△ABE∽△DEF.
∴∠ABE=∠DEF.
∵∠ABE+∠AEB=90°,
∴∠DEF+∠AEB=90°,
∴∠BEF=90°,
∴BE⊥EF且BE=2EF.
分析:根据题意画出符合题意的图形,根据相似三角形的判定方法可证明△AEB∽△DFE,再由相似三角形的性质:对应角相等对应边的比值相等可证明BE⊥EF,BE=2EF.
点评:本题考查了相似三角形的判定和性质、正方形的性质、勾股定理的运用,也考查了学生的猜想能力,题目难度不大,但很新颖.
 理由如下:
理由如下:∵四边形ABCD是正方形,
∴∠A=90°,
∵E是AD的中点,
∴AE=
 AD=
AD= ×4=2,
×4=2,∴由勾股定理得:BE=
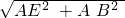 =2
=2 ,
,同理在直角三角形DEF中,DE=2,DF=1,EF=
 ,
,∵
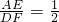 ,
,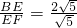 =
= ,
,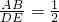 ,
,∴
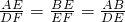 ,
,∴△ABE∽△DEF.
∴∠ABE=∠DEF.
∵∠ABE+∠AEB=90°,
∴∠DEF+∠AEB=90°,
∴∠BEF=90°,
∴BE⊥EF且BE=2EF.
分析:根据题意画出符合题意的图形,根据相似三角形的判定方法可证明△AEB∽△DFE,再由相似三角形的性质:对应角相等对应边的比值相等可证明BE⊥EF,BE=2EF.
点评:本题考查了相似三角形的判定和性质、正方形的性质、勾股定理的运用,也考查了学生的猜想能力,题目难度不大,但很新颖.

练习册系列答案
相关题目
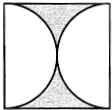 如图,在边长为a的正方形铁块中,以两对边中点为圆心,以a为直径截取两个半圆,求余下废料的面积是多少?
如图,在边长为a的正方形铁块中,以两对边中点为圆心,以a为直径截取两个半圆,求余下废料的面积是多少?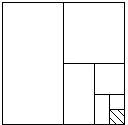 我国著名的数学家华罗庚曾说过:“数形结合百般好,割裂分家万事非”,如图,在边长为1的正方形纸板上,依次贴上面积为
我国著名的数学家华罗庚曾说过:“数形结合百般好,割裂分家万事非”,如图,在边长为1的正方形纸板上,依次贴上面积为
 在边长为16cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个无盖的长方体.
在边长为16cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个无盖的长方体.