Question

如图，扇形OAB中，∠AOB=90°，半径OA=1，C是线段AB的中点，CD∥OA，交弧AB于点D，则CD=______．

Answer 1

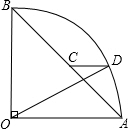
延长DC，交OB于点E，
∵CD∥OA，∠AOB=90°，
∴∠DEO=∠AOB=90°，
∵OD=OA=1，
C是线段AB中点，
∴CE是△AOB的中位线，
∴OE=EB=

1

2

，
根据勾股定理得：DE=

3

2

，
CE=

1

2

OA=

1

2

，
∴CD=DE-CE=

3 -1

2

．
故答案为：

3 -1

2

．