题目内容
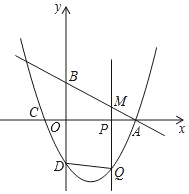
【题目】感知:如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() 点
点![]() 分别在边
分别在边![]() 上,
上,![]() 连接
连接![]() 点
点![]() 分别为
分别为![]() 的中点,则
的中点,则![]() 与
与![]() 的数量关系是: .
的数量关系是: .
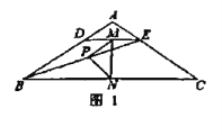
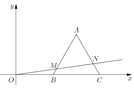
探究:把![]() 绕点
绕点![]() 顺时针方向旋转,如图
顺时针方向旋转,如图![]() ,连接
,连接![]()
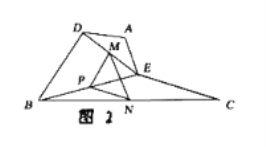
![]() 证明:
证明: ![]()
![]() 的度数为 _
的度数为 _![]()
应用:把![]() 绕点
绕点![]() 在平面内自由旋转,若
在平面内自由旋转,若![]() 面积的最大值为___________.
面积的最大值为___________.
【答案】感知:![]() ;探究:
;探究:![]() 详见解析;
详见解析;![]() ;
; ![]()
【解析】
感知:由题意可得BD=CE,由三角形中位线可得BD=2PM,CE=2PN,可得PM=PN;
探究:(1)由“SAS”可证![]() ,由三角形中位线定理可得BD=2PM,CE=2PN,可得PM=PN;
,由三角形中位线定理可得BD=2PM,CE=2PN,可得PM=PN;
(2)由全等三角形的性质可得∠ABD=∠ACE,由平行线的性质可得∠BDE=∠MPE,∠BNP=∠BCE,由三角形外角性质可求∠MPN=60°,可证△PMN是等边三角形,即可求解;
应用:先判断出BD最大时,△PMN的面积最大,而BD最大值是AB+AD=12,即可求解.
解:感知:∵AB=AC,AD=AE
∴BD=CE
∴ BD=2PM,CE=2PN
∴PM=PN
故答案为PM=PN.
探究:
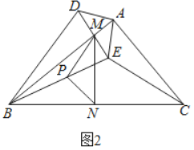
![]() 证明:
证明:![]()
![]()
又![]() .
.
![]() (SAS).
(SAS).
![]() .
.
![]() 点
点![]() 分别是
分别是![]() 的中点,
的中点,
![]()
![]() 点
点![]() 分别是
分别是![]() 的中点
的中点
![]() .
.
![]()
(2)∵![]()
∴∠ABD=∠ACE
∵PM=PN
∴△PMN是等腰三角形
∵PM∥BD
∴∠DBE=∠MPE
∵PN∥BD
∴∠BNP=∠BCE
∵∠DBN=∠DBP+∠EBC=∠MPE+∠EBC
∴∠MPN=∠MPE+∠EPN=∠MPE+∠EBC+∠PNB=∠DBN+∠BCE=∠ABC+∠ABD+∠BCE=∠ABC+∠ACE+∠BCE=∠ABC+∠ACB
∴∠BAC=120°
∴∠ACB+∠ABC=60°
∴∠MPN=60°
∴△PMN是等边三角形
∴∠PMN=60°
故答案为60°.
(3)由(2)知△PMN是等边三角形,PM=PN=![]() BD
BD
∴PM最大时,△PMN面积最大,PM最小时,△PMN面积最小
∴点D在BA的延长线上,△PMN的面积最大
∴BD=AB+AD=12
∴PM=6
∴![]()
故答案为![]() .
.

【题目】某商场同时购进甲、乙两种商品共100件,其进价和售价如下表:
商品名称 | 甲 | 乙 |
进价(元/件) | 40 | 90 |
售价(元/件) | 60 | 120 |
设其中甲种商品购进x件,商场售完这100件商品的总利润为y元.
(Ⅰ)写出y关于x的函数关系式;
(Ⅱ)该商场计划最多投入8000元用于购买这两种商品,
①至少要购进多少件甲商品?
②若销售完这些商品,则商场可获得的最大利润是多少元?