Question

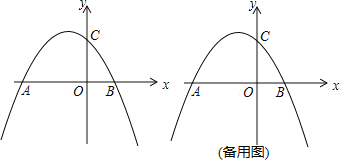
【题目】如图，二次函数的图象与轴交于点A、B，与y轴交于点C，点A的坐标为(-4,0)，P是抛物线上一点 （点P与点A、B、C不重合）．

（1）b=　　，点B的坐标是　　；

（2）设直线PB直线AC交于点M，是否存在这样的点P，使得PM:MB=1:2？若存在，求出点P的横坐标；若不存在，请说明理由；

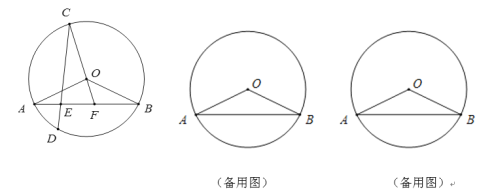
（3）连接AC、BC，判断∠CAB和∠CBA的数量关系，并说明理由．

Answer 1

【答案】（1）；（，0）；（2）存在点P的横坐标为或．（3）∠CBA=2∠CAB.理由见解析.

【解析】

（1）由点A的坐标，利用二次函数图象上点的坐标特征可求出b的值，代入y=0求出x值，进而可得出点B的坐标；

（2）（解法一）代入x=0求出y值，进而可得出点C的坐标，由点A、C的坐标利用待定系数法可求出直线AC的解析式，假设存在，设点M的坐标为（m，m+2），分B、P在直线AC的同侧和异侧两种情况考虑，由点B、M的坐标结合PM：MB=1：2即可得出点P的坐标，再利用二次函数图象上点的坐标特征可得出关于m的一元二次方程，解之即可得出结论；

（解法二）代入x=0求出y值，进而可得出点C的坐标，由点A、C的坐标利用待定系数法可求出直线AC的解析式，过点B作BB′∥y轴交直线AC于点B′，过点P作PP′∥y轴交直线AC于点P′，由点B的坐标可得出BB′的值，结合相似三角形的性质可得出PP′的值，设点P的坐标为（x，-x2-x+2），则点P′的坐标为（x，x+2），结合PP′的值可得出关于x的含绝对值符号的一元二次方程，解之即可得出结论；

（3）作∠CBA的角平分线，交y轴于点E，过点E作EF⊥BC于点F，设OE=n，则CE=2-n，EF=n，利用面积法可求出n值，进而可得出，结合∠AOC=90°=∠BOE可证出△AOC∽△BOE，根据相似三角形的性质可得出∠CAO=∠EBO，再根据角平分线的性质可得出∠CBA=2∠EBO=2∠CAB，此题得解．

（1）点在二次函数的图象上，

，

．

当时， 有，

解得：，，

点的坐标为，．

故答案为：；，．

（2） （方 法一） 当时，，

点的坐标为．

设直线的解析式为，

将、代入中，

得：，解得：，

直线的解析式为．

假设存在， 设点的坐标为．

①当点、在直线的异侧时， 点的坐标为，，

点在抛物线上，

，

整理， 得：．

△，

方程无解， 即不存在符合题意得点；

②当点、在直线的同侧时， 点的坐标为，，

点在抛物线上，

，

整理， 得：，

解得：，，

点的横坐标为或．

综上所述： 存在点，使得，点的横坐标为或．

（3），理由如下：

作的角平分线， 交轴于点，过点作于点，如图 2 所示 ．

点，，点，

，，．

设，则，，

由面积法， 可知：，即，

解得：．

，，

，

，

．