题目内容
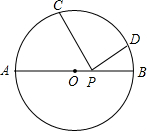 如图,已知圆O的面积为3π,AB为直径,弧AC的度数为80°,弧BD的度数为20°,点P为直径AB上任一点,则PC+PD的最小值为________.
如图,已知圆O的面积为3π,AB为直径,弧AC的度数为80°,弧BD的度数为20°,点P为直径AB上任一点,则PC+PD的最小值为________.
3
分析:先设圆O的半径为r,由圆O的面积为3π求出R的值,再作点C关于AB的对称点C′,连接OD,OC′,DC′,则DC′的长即为PC+PD的最小值,由圆心角、弧、弦的关系可知 =
= =80°,故BC′=100°,由
=80°,故BC′=100°,由 =20°可知
=20°可知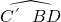 =120°,由OC′=OD可求出∠ODC′的度数,进而可得出结论.
=120°,由OC′=OD可求出∠ODC′的度数,进而可得出结论.
解答: 解:设圆O的半径为r,
解:设圆O的半径为r,
∵⊙O的面积为3π,
∴3π=πR2,即R= .
.
作点C关于AB的对称点C′,连接OD,OC′,DC′,则DC′的长即为PC+PD的最小值,
∵ 的度数为80°,
的度数为80°,
∴ =
= =80°,
=80°,
∴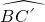 =100°,
=100°,
∵ =20°,
=20°,
∴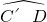 =
=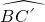 +
+ =100°+20°=120°,
=100°+20°=120°,
∵OC′=OD,
∴∠ODC′=30°
∴DC′=2OD•cos30°=2 ×
× =3,即PC+PD的最小值为3.
=3,即PC+PD的最小值为3.
故答案为:3.
点评:本题考查的是轴对称-最短路线问题及垂径定理,圆心角、弧、弦的关系,根据题意作出点C关于直线AB的对称点是解答此题的关键.
分析:先设圆O的半径为r,由圆O的面积为3π求出R的值,再作点C关于AB的对称点C′,连接OD,OC′,DC′,则DC′的长即为PC+PD的最小值,由圆心角、弧、弦的关系可知
 =
= =80°,故BC′=100°,由
=80°,故BC′=100°,由 =20°可知
=20°可知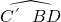 =120°,由OC′=OD可求出∠ODC′的度数,进而可得出结论.
=120°,由OC′=OD可求出∠ODC′的度数,进而可得出结论.解答:
 解:设圆O的半径为r,
解:设圆O的半径为r,∵⊙O的面积为3π,
∴3π=πR2,即R=
 .
.作点C关于AB的对称点C′,连接OD,OC′,DC′,则DC′的长即为PC+PD的最小值,
∵
 的度数为80°,
的度数为80°,∴
 =
= =80°,
=80°,∴
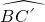 =100°,
=100°,∵
 =20°,
=20°,∴
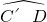 =
=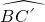 +
+ =100°+20°=120°,
=100°+20°=120°,∵OC′=OD,
∴∠ODC′=30°
∴DC′=2OD•cos30°=2
 ×
× =3,即PC+PD的最小值为3.
=3,即PC+PD的最小值为3.故答案为:3.
点评:本题考查的是轴对称-最短路线问题及垂径定理,圆心角、弧、弦的关系,根据题意作出点C关于直线AB的对称点是解答此题的关键.

练习册系列答案
相关题目
 相互垂直的弦,垂足为M.
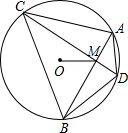
相互垂直的弦,垂足为M. 如图,已知圆O的半径OA=2,C为半径OB的中点,若∠AOB=90°,则图中阴影部分的面积为
如图,已知圆O的半径OA=2,C为半径OB的中点,若∠AOB=90°,则图中阴影部分的面积为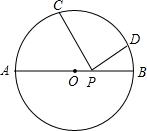 如图,已知圆O的面积为3π,AB为直径,弧AC的度数为80°,弧BD的度数为20°,点P为直径AB上任一点,则PC+PD的最小值为
如图,已知圆O的面积为3π,AB为直径,弧AC的度数为80°,弧BD的度数为20°,点P为直径AB上任一点,则PC+PD的最小值为 ,AB、CD是圆O的两条
,AB、CD是圆O的两条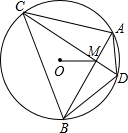 相互垂直的弦,垂足为M.
相互垂直的弦,垂足为M.