题目内容
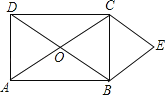
【题目】如图![]() ,平行四边形
,平行四边形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() .将直线
.将直线![]() 绕点
绕点![]() 顺时针旋转分别交
顺时针旋转分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
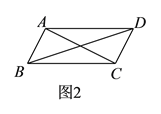
(![]() )在旋转过程中,线段
)在旋转过程中,线段![]() 与
与![]() 的数量关系是__________.
的数量关系是__________.
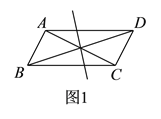
(![]() )如图
)如图![]() ,若
,若![]() ,当旋转角至少为__________
,当旋转角至少为__________![]() 时,四边形
时,四边形![]() 是平行四边形,并证明此时的四边形是
是平行四边形,并证明此时的四边形是![]() 是平行四边形.
是平行四边形.
【答案】(![]() )相等;(
)相等;(![]() )
)![]()
【解析】试题分析:(1)根据平行四边形的对边平行可得AD∥BC,对角线互相平分可得OA=OC,再根据两直线平行,内错角相等求出∠1=∠2,然后利用“角边角”证明△AOF和△COE全等,根据全等三角形对应边相等即可得到AF=CE
(2)根据垂直的定义可得∠BAO=90°,然后求出∠BAO=∠AOF,再根据内错角相等,两直线平行可得AB∥EF,然后根据平行四边形的对边平行求出AF∥BE,再根据两组对边分别平行的四边形是平行四边形证明;
试题解析:
(![]() )相等,理由如下:
)相等,理由如下:
如图所示:
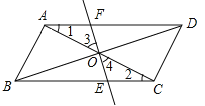
在ABCD中,AD∥BC,OA=OC,
∴∠1=∠2,
在△AOF和△COE中,
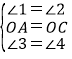
∴△AOF≌△COE(ASA),
∴AF=CE;
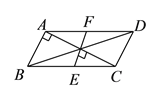
(![]() )证明:当旋转角为
)证明:当旋转角为![]() 时,
时,
![]() ,
,
又∵AB⊥AC,
∴∠BAO=90°,
∠AOF=90°,
∴∠BAO=∠AOF,
∴AB∥EF,
∵四边形ABCD是平行四边形,
∴AD∥BC,
即:AF∥BE,
∵AB∥EF,AF∥BE,
∴四边形ABEF是平行四边形;

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目