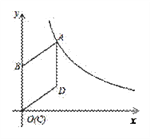
题目内容
【题目】在等腰![]() 和等腰
和等腰![]() 中,斜边
中,斜边![]() 中点
中点![]() 也是
也是![]() 的中点,
的中点,![]() ,
,![]() .
.
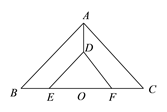
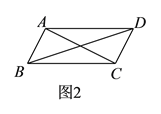
(![]() )如图,则
)如图,则![]() 与
与![]() 的关系是__________.
的关系是__________.
(![]() )将
)将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,请画出图形井求
,请画出图形井求![]() 的值.
的值.
(![]() )将
)将![]() 绕点
绕点![]() 逆时针旋转,角度为
逆时针旋转,角度为![]() ,请判断(
,请判断(![]() )的结论是否仍然成立,若成立请证明,若不成立请画图说明.
)的结论是否仍然成立,若成立请证明,若不成立请画图说明.
【答案】(![]() )相等且垂直;(
)相等且垂直;(![]() )
)![]() ;(
;(![]() )见解析
)见解析
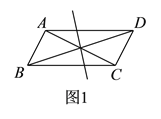
【解析】试题分析:(1)连接AO,A1O,如图1,根据等腰直角三角形的性质得AO⊥OC,AO=OC,A1O⊥OC1,OA1=OC1,则可判断A点、A1点、O点共线,于是得到AA1⊥C1C,AA1=C1C;
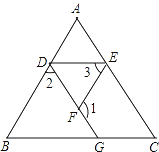
(2)先求得FG和GC,再在直角三角形GCF中根据![]() 求值;
求值;
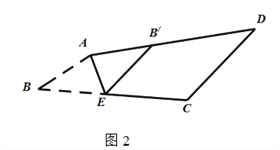
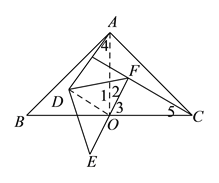
(3)连接OA,DO,如图2,利用旋转的性质得∠AOD=∠COF,则可利用“SAS”证明△OAD≌△OCF,所以AD=FC,∠OAD=∠OCF,再利用三角形内角和得到∠MHC=∠MOA=90°,于是得到AD⊥FC;
试题解析:
(1)连接AO,DO,如图所示:
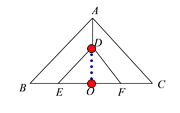
∵△ABC和△DEF都是等腰直角三角形,斜边EF中点O也是BC的中点,
∴AO⊥OC,AO=OC,DO⊥OF,OD=OF,
∴A点、D点、O点共线,
∴AD⊥FC,OA-OD=OC-OD,
∴AD=FC;
(![]() )∵旋转
)∵旋转
∴![]() .
.
∵等腰![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 为等腰
为等腰![]() .
.
在![]() 中
中
![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() 为
为![]() 中点,
中点,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]()
∴![]() .
.
∵![]() 为
为![]() 中点,
中点,
∴![]() ,
,
∴![]() .
.
在![]() 中,
中,![]()
∴![]() ,
,
∴![]() .
.
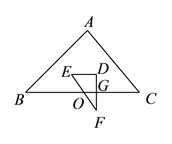
(![]() )连接
)连接![]() 、
、![]() .
.
∵等腰![]() ,
,![]() 为
为![]() 中点
中点
∴![]() ,
,![]()
∴![]() 为等腰
为等腰![]() ,
,
∴![]() .
.
∵等腰![]() ,
,![]() 为
为![]() 中点,
中点,
∴![]() ,
,![]() ,
,
∴![]() 为等腰
为等腰![]() ,
,
∴![]() .
.
∵![]()
∴![]() .
.
在![]() 和
和![]() 中
中
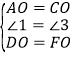 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,![]() .
.
∵![]()
∴![]()
∴![]() ,
,
∴(![]() )则结论仍成立.
)则结论仍成立.

练习册系列答案
相关题目