题目内容
已知:如图,等边△ABC的边长是4,在等边△ABC上再叠加一个Rt△DEF,∠DEF=90°,∠F=30°,等边△ABC的边BC与EF重合,顶点E与B重合,顶点A在DF上,(1)求边EF的长;
(2)若△ABC沿EF方向从E运动到F,速度为1m/s,时间为x秒,设Rt△DEF和等边△ABC重合部分的面积是y,请你写出y与x之间的函数关系式;
(3)重合部分的面积与Rt△DEF的面积的比有可能是7:24吗?如果有可能,请求出此时x的值;如果没有可能,请说明理由.

【答案】分析:(1)先根据△ABC是等边三角形可知∠ACB=60°,再由三角形外角的性质即可得出∠CAF=30°,故可得出AC=CF=4,故可得出EF的长;
(2)根据速度为1m/s,时间为x秒,可知BE=x,BF=8-x,再由△ABC是等边三角形可知∠A=60°,由∠F=30°得出∠ANM=90°,根据直角三角形的性质得出BN= BF=
BF= ,AN=4-BN=4-
,AN=4-BN=4- =
= ,再根据AM=2AN表示AM,由表示出AN、AM的长可用x表示出△AMN的面积,再由y=S△ABC-S△AMN即可得出结论;
,再根据AM=2AN表示AM,由表示出AN、AM的长可用x表示出△AMN的面积,再由y=S△ABC-S△AMN即可得出结论;
(3)根据Rt△DEF中,EF=8,∠F=30°可求出DE的长,进而根据重合部分的面积与Rt△DEF的面积的比有可能是7:24得出△DEF的面积,再由y与x的关系式即可得出结论.
解答:解:(1)∵△ABC是等边三角形,
∴∠ACB=60°,
∵∠ACB是△ACF的外角,∠F=30°,
∴∠CAF=∠ACB-∠F=60°-30°=30°,
∴AC=CF=4,
∴EF=BC+CF=4+4=8;
(2)∵速度为1m/s,时间为x秒,
∴BE=x,BF=8-x,
∵△ABC是等边三角形,
∴∠A=60°,
∵∠F=30°,
∴∠ANM=90°,
∴BN= BF=
BF= ;
;
∴AN=4-BN=4- =
= ,
,
∵由(1)知,∠AMN=∠F=30°,
∴AM=2AN=2× =x,
=x,
∴MN= x,
x,
∴S△AMN= AN•MN=
AN•MN= ×
× ×
× x=
x= x2,
x2,
∵△ABC是边长为4的等边三角形,
∴S△ABC= ×4×2
×4×2 =4
=4 ,
,
∴y=S△ABC-S△AMN=4 -
- x2(0≤x≤8);
x2(0≤x≤8);
(3)存在.
∵Rt△DEF中,EF=8,∠F=30°,
∴DE= ,
,
∴S△DEF= EF•DE=
EF•DE= ×8×
×8× =
= ,
,
∵由(2)知,y=4 -
- x2(0≤x≤8),
x2(0≤x≤8),
∴ =
= ,
,
解得x= 或x=-
或x=- (不合题意),
(不合题意),
∴存在重合部分的面积与Rt△DEF的面积的比是7:24.
点评:此题考查了相似性综合题,涉及的知识有:等边三角形的性质,含30度直角三角形的性质,三角形的面积求法,函数关系式的列法,熟练掌握等边三角形的性质是解本题的关键.
(2)根据速度为1m/s,时间为x秒,可知BE=x,BF=8-x,再由△ABC是等边三角形可知∠A=60°,由∠F=30°得出∠ANM=90°,根据直角三角形的性质得出BN=
 BF=
BF= ,AN=4-BN=4-
,AN=4-BN=4- =
= ,再根据AM=2AN表示AM,由表示出AN、AM的长可用x表示出△AMN的面积,再由y=S△ABC-S△AMN即可得出结论;
,再根据AM=2AN表示AM,由表示出AN、AM的长可用x表示出△AMN的面积,再由y=S△ABC-S△AMN即可得出结论;(3)根据Rt△DEF中,EF=8,∠F=30°可求出DE的长,进而根据重合部分的面积与Rt△DEF的面积的比有可能是7:24得出△DEF的面积,再由y与x的关系式即可得出结论.
解答:解:(1)∵△ABC是等边三角形,
∴∠ACB=60°,
∵∠ACB是△ACF的外角,∠F=30°,
∴∠CAF=∠ACB-∠F=60°-30°=30°,
∴AC=CF=4,
∴EF=BC+CF=4+4=8;
(2)∵速度为1m/s,时间为x秒,
∴BE=x,BF=8-x,
∵△ABC是等边三角形,
∴∠A=60°,
∵∠F=30°,
∴∠ANM=90°,
∴BN=
 BF=
BF= ;
;∴AN=4-BN=4-
 =
= ,
,∵由(1)知,∠AMN=∠F=30°,
∴AM=2AN=2×
 =x,
=x,∴MN=
 x,
x,∴S△AMN=
 AN•MN=
AN•MN= ×
× ×
× x=
x= x2,
x2,∵△ABC是边长为4的等边三角形,
∴S△ABC=
 ×4×2
×4×2 =4
=4 ,
,∴y=S△ABC-S△AMN=4
 -
- x2(0≤x≤8);
x2(0≤x≤8);(3)存在.
∵Rt△DEF中,EF=8,∠F=30°,
∴DE=
 ,
,∴S△DEF=
 EF•DE=
EF•DE= ×8×
×8× =
= ,
,∵由(2)知,y=4
 -
- x2(0≤x≤8),
x2(0≤x≤8),∴
 =
= ,
,解得x=
 或x=-
或x=- (不合题意),
(不合题意),∴存在重合部分的面积与Rt△DEF的面积的比是7:24.
点评:此题考查了相似性综合题,涉及的知识有:等边三角形的性质,含30度直角三角形的性质,三角形的面积求法,函数关系式的列法,熟练掌握等边三角形的性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 明理由;
明理由; 已知:如图,等边△ABC的边长为6,点D、E分别在AB、AC上,且AD=AE=2,直线l过点A,且l∥BC,若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设F点运动的时间为t秒,当t>0时,直线DF交l于点G,GE的延长线与BC的延长线交于点H,AB与GH相交于点O.
已知:如图,等边△ABC的边长为6,点D、E分别在AB、AC上,且AD=AE=2,直线l过点A,且l∥BC,若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设F点运动的时间为t秒,当t>0时,直线DF交l于点G,GE的延长线与BC的延长线交于点H,AB与GH相交于点O. 已知,如图,等边三角形ABC边长为2,以BC为对称轴将△ABC翻折,得到四边形ABDC,将此四边形放在直角坐标系xOy中,使AB在x轴上,点D在直线
已知,如图,等边三角形ABC边长为2,以BC为对称轴将△ABC翻折,得到四边形ABDC,将此四边形放在直角坐标系xOy中,使AB在x轴上,点D在直线 已知:如图,等边△ABC的边长为2,E为BC边的中点,分别以顶点B、C为圆心,BE、CE长为半径画弧交AB、AC于点D、F.求图中阴影部分的面积.
已知:如图,等边△ABC的边长为2,E为BC边的中点,分别以顶点B、C为圆心,BE、CE长为半径画弧交AB、AC于点D、F.求图中阴影部分的面积. 已知:如图,等边三角形ABD与等边三角形ACE具有公共顶点A,连接CD,BE,交于点P.
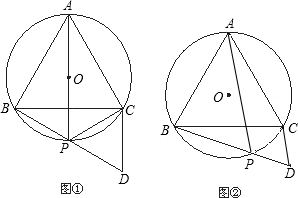
已知:如图,等边三角形ABD与等边三角形ACE具有公共顶点A,连接CD,BE,交于点P.