题目内容
在直角坐标系xOy中,一次函数y=k1x+b的图象与反比例函数 的图象交于A(1,4)、B(3,m)两点.
的图象交于A(1,4)、B(3,m)两点.
(1)求一次函数的解析式;
(2)求△AOB的面积.
(3)当x取何值时,反比例函数的值大于一次函数的值.(直接写出答案)
解:(1)∵反比例函数y=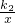 的图象过A(1,4)、B(3,m)两点
的图象过A(1,4)、B(3,m)两点
∴
∴ ;
;
所以一次函数y=k1x+b的图象过点A(1,4)、B(3, )两点,
)两点,
∴ ,
,
解得 ,
,
∴一次函数的解析式为y=- x+
x+ ;
;
(2)设一次函数图象与与x轴相交于C,
则C的坐标为(4,0),
则S△OAB=S△OAC-S△OBC
= (4-
(4- )×4
)×4
= ;
;
(3)根据图象知道:
当0<x<1 或 x>3,反比例函数的值大于一次函数的值.
分析:(1)首先利用A的坐标确定反比例函数的解析式,然后利用解析式确定B的坐标,接着利用待定系数法确定一次函数的解析式;
(2)如图,根据图象可以知道S△OAB=S△OAC-S△OBC,所以首先利用一次函数的解析式求出C的坐标,然后利用A、B、C的坐标和三角形的面积公式即可解决问题;
(3)利用函数图象可以直观得到反比例函数的值大于一次函数的值的对应的x的取值范围.
点评:此题分别考查了待定系数法确定函数的解析式、三角形的面积公式及一次函数与一元一次不等式的解集的关系,同时也利用数形结合的思想解决问题.
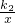 的图象过A(1,4)、B(3,m)两点
的图象过A(1,4)、B(3,m)两点
∴

∴
 ;
;所以一次函数y=k1x+b的图象过点A(1,4)、B(3,
 )两点,
)两点,∴
 ,
,解得
 ,
,∴一次函数的解析式为y=-
 x+
x+ ;
;(2)设一次函数图象与与x轴相交于C,
则C的坐标为(4,0),
则S△OAB=S△OAC-S△OBC
=
 (4-
(4- )×4
)×4=
 ;
;(3)根据图象知道:
当0<x<1 或 x>3,反比例函数的值大于一次函数的值.
分析:(1)首先利用A的坐标确定反比例函数的解析式,然后利用解析式确定B的坐标,接着利用待定系数法确定一次函数的解析式;
(2)如图,根据图象可以知道S△OAB=S△OAC-S△OBC,所以首先利用一次函数的解析式求出C的坐标,然后利用A、B、C的坐标和三角形的面积公式即可解决问题;
(3)利用函数图象可以直观得到反比例函数的值大于一次函数的值的对应的x的取值范围.
点评:此题分别考查了待定系数法确定函数的解析式、三角形的面积公式及一次函数与一元一次不等式的解集的关系,同时也利用数形结合的思想解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

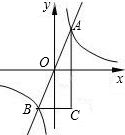 在直角坐标系xoy中,函数y=4x的图象与反比例函数y=
在直角坐标系xoy中,函数y=4x的图象与反比例函数y= (2012•北京二模)已知:如图,在直角坐标系xOy中,点A(8,0)、B(0,6),点C在x轴的负半轴上,AB=AC.动点M在x轴上从点C向点A移动,动点N在线段AB上从点A向点B移动,点M、N同时出发,且移动的速度都为每秒1个单位,移动时间为t秒(0<t<10).
(2012•北京二模)已知:如图,在直角坐标系xOy中,点A(8,0)、B(0,6),点C在x轴的负半轴上,AB=AC.动点M在x轴上从点C向点A移动,动点N在线段AB上从点A向点B移动,点M、N同时出发,且移动的速度都为每秒1个单位,移动时间为t秒(0<t<10). 析式为y=x2-mx+n.方程x2-mx+n=0的两根倒数和为-4.
析式为y=x2-mx+n.方程x2-mx+n=0的两根倒数和为-4.