Question

【题目】数轴上点表示的数是，点表示的数是，则线段的长表示为.例如：数轴上点表示的数是5，点表示的数是2，则线段的长表示为．

（1）点表示的数是3，线段的长可表示为______．

（2）若，______．

（3）数轴上的任意一点表示的数是，且的最小值为5，若，则的值为______．

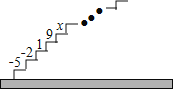
（4）如图，在数轴上点在点的右边，，若代数式与互为相反数，求的值．

Answer 1

【答案】（1）；（2）a=3或-1；（3）b=-2或8；（4）m的值为或.

【解析】

（1）根据题意，线段的长度即为数轴上两点表示的数的差的绝对值，可知线段CA的长可表示为；

（2）由，可知点A与点1之间的长度为2，则根据数轴上两点之间的距离即可得；

（3）由的最小值为5，可知点P在数轴上表示数和数b的两点之间的点，即AB距离为5，代入a值即可求出b；

（4）由数轴上点在点的右边可知a>b，结合，需要分情况讨论，解出a、b值代入代数式，利用两数互为相反数和为0列出关于m的一次方程式求解即可．

（1）根据题意知，=，

故答案为：；

（2）由，可知点A与点1之间的长度为2，利用数轴可以得出有两个值，分别在1的左侧和右侧，即=1+2=3或者=1-2=-1，

故答案为：3或-1；

（3）由的最小值为5，可得x在数和数b之间，

∴，

∵，

∴3-b=5，

∴b=-2或b=8，

故答案为：-2或8；

（4）∵点在点的右边，，，

∴a>b，b=4a，

∴，解得，

或，解得，

∵+=0，

∴，

当a=-5，b=-20时，

，

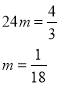
当a=3，b=-12时，

，

∴或，

故答案为：或．