题目内容
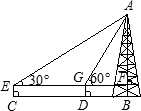 如图,小明所在学习小组的同学在测量塔高AB时,选择与塔底在同一水平面的同一直线上的C、D两点,用测角仪器测得塔顶A的仰角分别是30°和60°.已知测角仪器高CE=1.4米,CD=26米.求塔高AB.
如图,小明所在学习小组的同学在测量塔高AB时,选择与塔底在同一水平面的同一直线上的C、D两点,用测角仪器测得塔顶A的仰角分别是30°和60°.已知测角仪器高CE=1.4米,CD=26米.求塔高AB.(参考数据:
| 2 |
| 3 |
分析:先根据题意得出∠AEG=30°,∠AGF=60°,AF⊥EF,BF=CE=1.4米,进而求出∠EAG的度数及AG的长,在Rt△AGF中利用锐角三角函数的定义即可求出AF的长,进而可得出AB的长.
解答:解:依题意,得∠AEG=30°,∠AGF=60°,AF⊥EF,BF=CE=1.4米.
∴∠EAG=∠AGF-∠AEG=60°-30°=30°.(1分)
∴AG=EG=CD=26.(2分)
在Rt△AGF中,sin∠AGF=
,
∴AF=AG•sin∠AGF=26•sin60°=26×
=13
.(3分)
∴AB=AF+BF=13
+1.4≈23.916.(4分)
答:塔高AB为23.916米.(5分)
∴∠EAG=∠AGF-∠AEG=60°-30°=30°.(1分)
∴AG=EG=CD=26.(2分)
在Rt△AGF中,sin∠AGF=
| AF |
| AG |
∴AF=AG•sin∠AGF=26•sin60°=26×
| ||
| 2 |
| 3 |
∴AB=AF+BF=13
| 3 |
答:塔高AB为23.916米.(5分)
点评:本题考查的是解直角三角形的应用-仰角俯角问题,解答此类问题的关键是找出符合条件的直角三角形,利用锐角三角函数的定义进行解答.

练习册系列答案
相关题目
 如图,小明所在学习小组的同学在测量塔高AB时,选择与塔底在同一水平面的同一直线上的C、D两点,用测角仪器测得塔顶A的仰角分别是30°和60°.已知测角仪器高CE=1.4米,CD=26米.求塔高AB.
如图,小明所在学习小组的同学在测量塔高AB时,选择与塔底在同一水平面的同一直线上的C、D两点,用测角仪器测得塔顶A的仰角分别是30°和60°.已知测角仪器高CE=1.4米,CD=26米.求塔高AB. )
) )
)

 )
)