题目内容
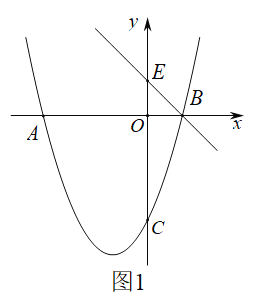
【题目】直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,抛物线
,抛物线![]() 经过点
经过点![]() 、点
、点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线![]() 的解析式;
的解析式;
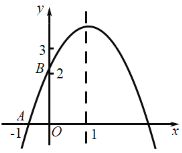
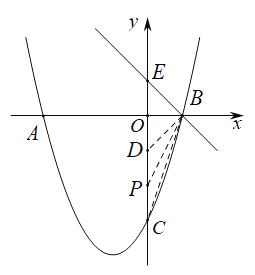
(2)如图1,点![]() 在
在![]() 轴上,连接
轴上,连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
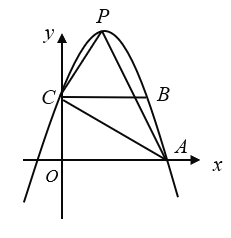
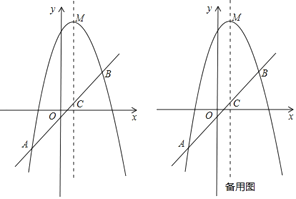
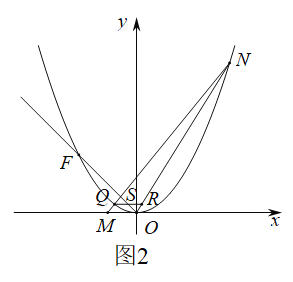
(3)如图2,将抛物线![]() 平移,使其顶点是坐标原点
平移,使其顶点是坐标原点![]() ,得到抛物线
,得到抛物线![]() ,平移直线
,平移直线![]() 经过原点
经过原点![]() ,交抛物线
,交抛物线![]() 于点
于点![]() .点
.点![]() ,点
,点![]() 是
是![]() 第一象限内一动点,
第一象限内一动点,![]() 交
交![]() 于
于![]() 点,
点,![]() 轴分别交
轴分别交![]() 、
、![]() 于
于![]() 、
、![]() ,试探究
,试探究![]() 与
与![]() 之间的数量关系.
之间的数量关系.
【答案】(1)![]() ;(2)
;(2)![]() 、
、![]() ;(3)
;(3)![]()
【解析】
(1)先求出点B的坐标,利用待定系数法即可求出抛物线的解析式;
(2)先在![]() 轴负半轴上取一点
轴负半轴上取一点![]() ,使
,使![]() ,证明
,证明![]() 即可求出OP得到点P的坐标;
即可求出OP得到点P的坐标;
(3)求出直线![]() 的解析式为y=nx,直线
的解析式为y=nx,直线![]() 的解析式
的解析式![]() ,联立
,联立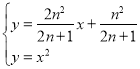 求得点
求得点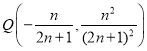 ,利用
,利用![]() 轴分别交
轴分别交![]() 、
、![]() 于
于![]() 、
、![]() ,求出
,求出 ,
,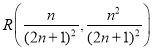 ,得到
,得到![]() ,
,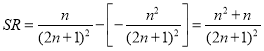 ,即可证得结论QS=SR.
,即可证得结论QS=SR.
解:(1)在y=-x+1中,令![]() ,得
,得![]() ,
,
∴![]() ,
,
∵![]() 经过点
经过点![]() 、点
、点![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴抛物线![]() 的解析式为:
的解析式为:![]() .
.
(2)在y=-x+1中,令![]() ,得
,得![]() ,
,
∴![]() ,
,
在![]() 中,令
中,令![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 轴负半轴上取一点
轴负半轴上取一点![]() ,使
,使![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
根据对称性知![]() 也符合要求.
也符合要求.
综上所述,符合条件的点![]() 的坐标为
的坐标为![]() 、
、![]() .
.
(3)依题意知:抛物线![]() 的解析式为
的解析式为![]() ,直线
,直线![]() 的解析式为
的解析式为![]() ,
,
∴![]() ,
,
设![]() ,∵
,∵![]() ,
,
∴直线![]() 的解析式为y=nx,
的解析式为y=nx,
直线![]() 的解析式
的解析式![]() ,
,
联立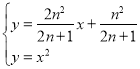 ,
,
消去![]() 整理得
整理得![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴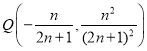 ,
,
∵![]() 轴分别交
轴分别交![]() 、
、![]() 于
于![]() 、
、![]() ,
,
∴ ,
,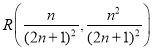 ,
,
∴![]() ,
,
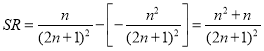 ,
,
∴![]() .
.


练习册系列答案
相关题目