题目内容
如图，P是⊙O的直径AB延长线上一点，PC切⊙O于点C，PC=6，BC：AC=1：2，则AB的长为________．
9
分析：PC切⊙O于点C，则得到∠PCB=∠A，易证△PCB∽△PAC，因而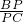
=
=
，因而求得BP=，PC=3，根据切割线定理得到PC2=PB•PA，可求PA=12，所以AB=9．
解答：PC切⊙O于点C，则∠PCB=∠A，∠P=∠P，
∴△PCB∽△PAC，
∴==
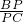∵BP=PC=3，
∴PC2=PB•PA，即36=3•PA，
∵PA=12
∴AB=12-3=9．
点评：此题综合考查函数、方程与圆的切线，三角形相似的判定与性质等知识．
分析：PC切⊙O于点C，则得到∠PCB=∠A，易证△PCB∽△PAC，因而
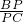==，因而求得BP=，PC=3，根据切割线定理得到PC2=PB•PA，可求PA=12，所以AB=9．解答：PC切⊙O于点C，则∠PCB=∠A，∠P=∠P，
∴△PCB∽△PAC，
∴
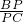==∵BP=
PC=3，∴PC2=PB•PA，即36=3•PA，
∵PA=12
∴AB=12-3=9．
点评：此题综合考查函数、方程与圆的切线，三角形相似的判定与性质等知识．
练习册系列答案
相关题目
如图，AB是⊙O的直径，点D在AB的延长线上，过点D作⊙O的切线，切点为C，若∠A=35°，则∠D=
如图，AC是⊙O的直径，BD是⊙O的弦，EC∥AB，交⊙O于E．图中与∠BOC的一半相等的角有
如图，AB是⊙O的直径，D为弧AC的中点，∠B=50°，则∠DAC=
如图，AB是⊙O的直径，∠ABC=30°，OA=2，则BC长为
如图：P是⊙O的直径BA延长线上一点，PD交⊙O于点C，且PC=OD，如果∠P=24°，则∠DOB=