��Ŀ����
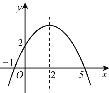
����Ŀ����֪����ƽ��ֱ������ϵ�У�![]() Ϊ
Ϊ![]() �Ḻ�����ϵĵ㣬
�Ḻ�����ϵĵ㣬![]() Ϊ
Ϊ![]() �Ḻ�����ϵĵ�.
�Ḻ�����ϵĵ�.
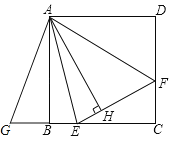
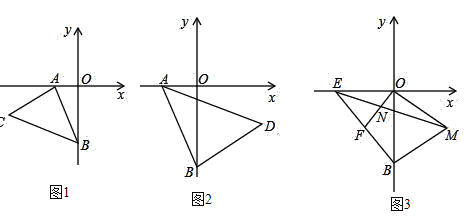
(1)��ͼ1����![]() ��Ϊ���㡢
��Ϊ���㡢![]() Ϊ���ڵ�������������
Ϊ���ڵ�������������![]() ����
����![]() ��
��![]() ������
������![]() ������ꣻ
������ꣻ
(2)��ͼ![]() ������
������![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ����
����![]() ��������Ϊ
��������Ϊ![]() ����
����![]() Ϊ���㣬
Ϊ���㣬![]() Ϊ��������
Ϊ��������![]() .���ʣ���
.���ʣ���![]() ����
����![]() �Ḻ���������˶�����������������ʱ����ʽ
�Ḻ���������˶�����������������ʱ����ʽ![]() ��ֵ�Ƿ����仯�����������仯���������ֵ���������仯����˵�����ɣ�
��ֵ�Ƿ����仯�����������仯���������ֵ���������仯����˵�����ɣ�
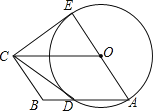
(3)��ͼ![]() ��
��![]() Ϊ
Ϊ![]() �Ḻ�����ϵ�һ�㣬��
�Ḻ�����ϵ�һ�㣬��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() Ϊ�����ȱ�
Ϊ�����ȱ�![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ����̽�������߶�
����̽�������߶�![]() ��
��![]() ��
��![]() �У������߶ε���
�У������߶ε���![]() ��
��![]() �IJ��һ�룿����д�����������ϵ��������֤��.
�IJ��һ�룿����д�����������ϵ��������֤��.
���𰸡�(1) C(-6,-2);(2)�������仯��ֵΪ![]() ����3��EN=
����3��EN=![]() (EM-ON)��֤�������.
(EM-ON)��֤�������.
��������
��1����CQ��OA�ڵ�Q,����֤��![]() ����QC=AD,AQ=BO,���������Ϳ��������C�����ꣻ
����QC=AD,AQ=BO,���������Ϳ��������C�����ꣻ
��2����DP��OB�ڵ�P������֤��![]() ������BP=OB-PO=m-(-n)=m+nΪ��ֵ���Ӷ������������
������BP=OB-PO=m-(-n)=m+nΪ��ֵ���Ӷ������������![]() ��ֵ����Ϊ
��ֵ����Ϊ![]() .
.
��3����BH��EB�ڵ�B�����������Եó���1=30��,��2=��3=��EMO=15��,��EOF=��BMG=45��,EO=BM,����֤��![]() ����GM=ON,����EM-ON=EM-GM=EG,�����ƽ���߷��߶γɱ��������Ϳɵó�EN=
����GM=ON,����EM-ON=EM-GM=EG,�����ƽ���߷��߶γɱ��������Ϳɵó�EN=![]() (EM-ON).
(EM-ON).
��1����ͼ��1����CQ��OA��Q,
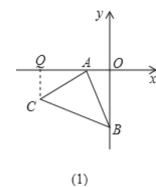
���AQC=90��,
��![]() Ϊ����ֱ�������Σ�
Ϊ����ֱ�������Σ�
��AC=AB,��CAB=90��,
���QAC+��OAB=90��,
�ߡ�QAC+��ACQ=90��,
���ACQ=��BAO,
����AC=AB,��AQC=��AOB,
��![]() (AAS),
(AAS),
��CQ=AO,AQ=BO,
��OA=2,OB=4,
��CQ=2,AQ=4,
��OQ=6,
��C(-6,-2).
(2)��ͼ��2����DP��OB�ڵ�P,
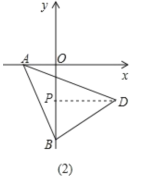
���BPD=90��,
��![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�
��AB=BD,��ABD=��ABO+��OBD=90��,
�ߡ�OBD+��BDP=90��,
���ABO=��BDP,
����AB=BD,��AOB=��BPD=90��,
��![]()
��AO=BP,
��BP=OB-PO=m-(-n)=m+n,
��A![]() ,
,
��OA=![]() ,
,
��m+n=![]() ,
,
������B��y�Ḻ���������˶�ʱ��AO=BP=m+n=![]() ,
,
����ʽ![]() ��ֵ����Ϊ
��ֵ����Ϊ![]() .
.
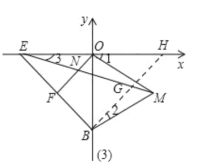
��3��![]()
֤������ͼ��3����ʾ����ME��ȡһ��Gʹ��MG=ON,����BG���ӳ�����x����H.
��![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�
��BO=BM=MO,��OBM=��OMB=��BOM=60��,
��EO=MO,��EBM=105��,��1=30��,
��OE=OB,
��OE=OM=BM,
���3=��EMO=15��,
���BEM=30��,��BME=45��,
��OF��EB,
���EOF=��BME,
��![]() ,
,
��BG=EN,
��ON=MG,
���2=��3,
���2=15��,
���EBG=90��,
��BG=![]() EG,
EG,
��EN=![]() EG,
EG,
��EG=EM-GM,
��EN=![]() (EM-GM),
(EM-GM),
��EN=![]() (EM-ON).
(EM-ON).

 ����ʦ���һ��һ��ϵ�д�
����ʦ���һ��һ��ϵ�д� �Ͻ�ƽ��У����ϵ�д�
�Ͻ�ƽ��У����ϵ�д�