题目内容
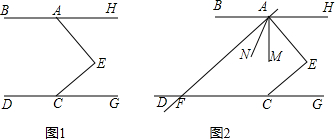
如图，A、B在直线MN的同侧，在直线MN上求一点P，使∠APM=∠BPN．分析：作点A关于直线MN的对称点A′，连接A′B交MN于点P，根据轴对称的性质可得AP=A′P，∠APM=∠A′PM，再根据对顶角相等可得∠A′PM=∠BPN，从而得到∠APM=∠BPN，点P即为所求作的点．
解答：解：如图，作点A关于直线MN的对称点A′，连A′B交MN于P，
点P即为所求作的点．
点P即为所求作的点．
点评：本题考查了利用轴对称变换作图，熟记轴对称的性质并确定找出点A关于直线MN的对称点是解题的关键．
练习册系列答案
一本好题口算题卡系列答案
相关题目
36、已知如图，一辆汽车在直线公路AB上由A向B行驶，M，N分别是位于公路AB两侧的村庄．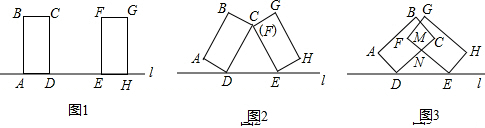
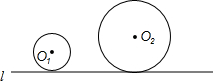（2013•嘉定区二模）已知⊙O1的半径长为2cm，⊙O2的半径长为4cm．将⊙O1、⊙O2放置在直线l上（如图），如果⊙O1在直线l上任意滚动，那么圆心距O1O2的长不可能是（ ）
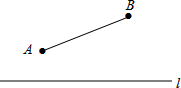如图，A、B在直线l的同侧，在直线l上求一点P，使△PAB的周长最小．