题目内容
 冰冰和亮亮想测量设在某建筑物顶上的广告牌离地面的高度.如图,他俩分别站在这座建筑物的两侧,并所站的位置与该建筑物在同一条直线上,相距110米,他们分别测得仰角分别是39°和28°,已知测角仪的高度是1米,试求广告牌离地面的高度(精确到1米).
冰冰和亮亮想测量设在某建筑物顶上的广告牌离地面的高度.如图,他俩分别站在这座建筑物的两侧,并所站的位置与该建筑物在同一条直线上,相距110米,他们分别测得仰角分别是39°和28°,已知测角仪的高度是1米,试求广告牌离地面的高度(精确到1米).
【答案】分析:首先分析图形:根据题意构造直角三角形;本题涉及到两个直角三角形△ACD、△BDC,应利用其公共边DC,及AB=AD+DB;解三角形可得方程关系式,进而可解即可求出答案.
解答:解:设CD长为x米
在Rt△ACD中cot39°= ,得AD=CDcot39°≈1.2x,
,得AD=CDcot39°≈1.2x,
在Rt△CDE中,cot28°= ,得DB=CDcot28°≈1.9x,
,得DB=CDcot28°≈1.9x,
又∵AD+BD=110,
∴1.2x+1.9x=110,
x≈35米.
∴CE=CD+DE=35+1=36米.
答:广告牌离地面的高度约为36米.
点评:本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.
解答:解:设CD长为x米
在Rt△ACD中cot39°=
 ,得AD=CDcot39°≈1.2x,
,得AD=CDcot39°≈1.2x,在Rt△CDE中,cot28°=
 ,得DB=CDcot28°≈1.9x,
,得DB=CDcot28°≈1.9x,又∵AD+BD=110,
∴1.2x+1.9x=110,
x≈35米.
∴CE=CD+DE=35+1=36米.
答:广告牌离地面的高度约为36米.
点评:本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
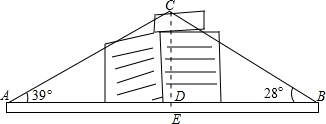 冰冰和亮亮想测量设在某建筑物顶上的广告牌离地面的高度.如图,他俩分别站在这座建筑物的两侧,并所站的位置与该建筑物在同一条直线上,相距110米,他们分别测得仰角分别是39°和28°,已知测角仪的高度是1米,试求广告牌离地面的高度(精确到1米).
冰冰和亮亮想测量设在某建筑物顶上的广告牌离地面的高度.如图,他俩分别站在这座建筑物的两侧,并所站的位置与该建筑物在同一条直线上,相距110米,他们分别测得仰角分别是39°和28°,已知测角仪的高度是1米,试求广告牌离地面的高度(精确到1米). 冰冰和亮亮想测量设在某建筑物顶上的广告牌离地面的高度.如图,他俩分别站在这座建筑物的两侧,并所站的位置与该建筑物在同一条直线上,相距110米,他们分别测得仰角分别是39°和28°,已知测角仪的高度是1米,试求广告牌离地面的高度(精确到1米).
冰冰和亮亮想测量设在某建筑物顶上的广告牌离地面的高度.如图,他俩分别站在这座建筑物的两侧,并所站的位置与该建筑物在同一条直线上,相距110米,他们分别测得仰角分别是39°和28°,已知测角仪的高度是1米,试求广告牌离地面的高度(精确到1米). 冰冰和亮亮想测量设在某建筑物顶上的广告牌离地面的高度.如图,他俩分别站在这座建筑物的两侧,并所站的位置与该建筑物在同一条直线上,相距110米,他们分别测得仰角分别是39°和28°,已知测角仪的高度是1米,试求广告牌离地面的高度(精确到1米).
冰冰和亮亮想测量设在某建筑物顶上的广告牌离地面的高度.如图,他俩分别站在这座建筑物的两侧,并所站的位置与该建筑物在同一条直线上,相距110米,他们分别测得仰角分别是39°和28°,已知测角仪的高度是1米,试求广告牌离地面的高度(精确到1米). 冰冰和亮亮想测量设在某建筑物顶上的广告牌离地面的高度.如图,他俩分别站在这座建筑物的两侧,并所站的位置与该建筑物在同一条直线上,相距110米,他们分别测得仰角分别是39°和28°,已知测角仪的高度是1米,试求广告牌离地面的高度(精确到1米).
冰冰和亮亮想测量设在某建筑物顶上的广告牌离地面的高度.如图,他俩分别站在这座建筑物的两侧,并所站的位置与该建筑物在同一条直线上,相距110米,他们分别测得仰角分别是39°和28°,已知测角仪的高度是1米,试求广告牌离地面的高度(精确到1米).