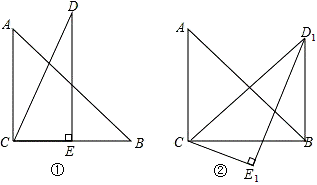
题目内容
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.
(1)求证:∠ACM=∠ABC;
(2)延长BC到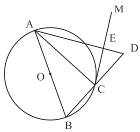 D,使BC = CD,连接AD与CM交于点E,若⊙O的半径为3
D,使BC = CD,连接AD与CM交于点E,若⊙O的半径为3 ,ED = 2,
,ED = 2,  求∆ACE的外接圆的半径.
求∆ACE的外接圆的半径.
证明:(1)连接OC
∵ AB为⊙O的直径
∴ ∠ACB = 90°
∴ ∠ABC +∠BAC = 90°[来源:]
又∵ CM是⊙O的切线
∴ OC⊥CM
∴ ∠ACM +∠ACO = 90°
∵ CO = AO
∴ ∠BAC =∠ACO
∴ ∠ACM =∠ABC
(2)∵ BC = CD
∴ OC∥AD
又∵ OC⊥CE
∴ AD⊥CE
∴ ΔAEC是直角三角形
∴ ΔAEC的外接圆的直径为AC
又∵ ∠ABC +∠BAC = 90°
∠ACM +∠ECD = 90°
而∠ABC =∠ACM
∴ ∠BAC =∠ECD
又∠CED =∠ACB = 90°
∴ ΔABC∽ΔCDE
∴ 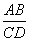 =
= 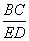
而⊙O的半径为3
∴ AB = 6
∴ 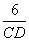 =
= 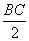
∴ BC2 = 12
∴ BC = 2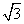 在RtΔABC中
在RtΔABC中
∴ AC = 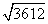 = 2
= 2
∴ ΔAEC的外接圆的半径为

练习册系列答案
相关题目
 式的变形正确的是
式的变形正确的是 B.
B. C.
C. D.
D.
 的图像与反比例函数
的图像与反比例函数 的图像交
的图像交 于
于 两点,点
两点,点 的横坐标为2.
的横坐标为2. 的值和点
的值和点 的象限,并说明理由.
的象限,并说明理由. ,则该等腰三角形的底角的度数为___ __________.
,则该等腰三角形的底角的度数为___ __________. ,并依据a的取值情况写出其解集.
,并依据a的取值情况写出其解集. >
>  C、x+3>y+3 D、-3x>-3y
C、x+3>y+3 D、-3x>-3y 。
。 加中考,为了了解这些考生的数学成绩,从中抽取2000名考生的数学成绩进行统计分析.在这个问题中,下列说法:
加中考,为了了解这些考生的数学成绩,从中抽取2000名考生的数学成绩进行统计分析.在这个问题中,下列说法: