题目内容
解方程:|x2-y2-4|+(3
x-5y-10)2=0的解是
,
,
.
| 5 |
|
|
|
|
分析:根据几个非负数和的性质得到
,利用代入消元法解方程组,由②得到y=
x-2③,把③代入①可得到x2-(
x-2)2-4=0,解方程得到x1=2
,x2=
,然后把x的值分别代入③即可得到原方程组的解.
|
3
| ||
| 5 |
3
| ||
| 5 |
| 5 |
| 5 |
解答:解:∵|x2-y2-4|+(3
x-5y-10)2=0,
∴
由②得y=
x-2③,
把③代入①得x2-(
x-2)2-4=0,
整理得x2-3
x+10=0,即(x-2
)(x-
)=0,
∴x1=2
,x2=
,
把x=2
代入③得y=
×2
-2=4,
把x=
代入③得y=
×
-2=1,
故原方程组的解为
,
.
故答案为
,
.
| 5 |
∴
|
由②得y=
3
| ||
| 5 |
把③代入①得x2-(
3
| ||
| 5 |
整理得x2-3
| 5 |
| 5 |
| 5 |
∴x1=2
| 5 |
| 5 |
把x=2
| 5 |
3
| ||
| 5 |
| 5 |
把x=
| 5 |
3
| ||
| 5 |
| 5 |
故原方程组的解为
|
|
故答案为
|
|
点评:本题考查了高次方程:利用换元法或因式分解的方法把高次方程转化为一元二次方程或一元一次方程求解.也考查了几个非负数和的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
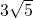 x-5y-10)2=0的解是________.
x-5y-10)2=0的解是________. x-5y-10)2=0的解是 .
x-5y-10)2=0的解是 .