题目内容

公式介绍：

1＋2＋3＋4＋5＋…＋n＝？

将另外1＋2＋3＋4＋5＋…＋n＝？与原来n＋(n－1)＋…＋3＋2＋1排在一起，拼成一个长为(n＋1)宽为n的矩形，总数为n＋(n＋1)个．所以可得1＋2＋3＋4＋5＋…＋n＝．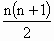

请你计算：①1＋2＋3＋4＋…＋2001＋2002＝________；

②1000＋1001＋1002＋…2001＋2002＝________．

答案：2005003,1505503
解析：

①2005003；②1505503．


练习册系列答案
相关题目
小王到玻璃店选购一块镶边框的矩形镜子，要求宽与长之比为1：2．售货员介绍镜子价格计算公式为：镜子总价（元）=镜面面积（平方米）×单价（a元/平方米）+边框长度（米）×单价（b元/米）+加工费（20元/块）．（边框宽度忽略不计）
（1）写出镜子的总价y（元）与矩形镜面宽x（米）之间的关系式（用含a、b的式子表示，不要求写出自变量取值范围）．
（2）售货员为小王计算了两种规格镜子的价格：①宽0.5米×长1米，总价为110元；②宽1米×长2米，总价为320元，请求出a和b的值．
（3）小王花了200元买回一块镜子，请你求出他购买的镜子的规格．
仔细阅读以下内容解决问题：
偏微分方程，对于多个变量的求最值问题相当有用，以2001年全国联赛第二试第一题为例给同学们作一介绍，问题建立数学模型后实际上是求：
y=5a2+6ab+3b2-30a-20b+46的最小值，先介绍求导公式，（xn）′=nxn-1，a′=0（a为常数），当ya′=10a+6b-30=0，yb′=6a+6b-20=0时，可取得最小值（ya′的意思是关于a求导，把b看作常数，（5a2）′=10a，（6ab）′=6b，（3a2-20b+46）′=0）．解方程，得a=
5
2
，b=
5
6
，代入可得y=
1
6
，即是最小值．
同学们：以上内容很有挑战性，确保读懂后请解答下面问题：运用阅读材料中的知识求s=4x2+2y2+4xy-12x-8y+17的最小值
7
7
．
仔细阅读以下内容解决问题：
偏微分方程，对于多个变量的求最值问题相当有用，以2001年全国联赛第二试第一题为例给同学们作一介绍，问题建立数学模型后实际上是求：
y=5a2+6ab+3b2-30a-20b+46的最小值，先介绍求导公式，（xn）′=nxn-1，a′=0（a为常数），当ya′=10a+6b-30=0，yb′=6a+6b-20=0时，可取得最小值（ya′的意思是关于a求导，把b看作常数，（5a2）′=10a，（6ab）′=6b，（3a2-20b+46）′=0）．解方程，得a=，b=，代入可得y=，即是最小值．
同学们：以上内容很有挑战性，确保读懂后请解答下面问题：运用阅读材料中的知识求s=4x2+2y2+4xy-12x-8y+17的最小值    ．
小王到玻璃店选购一块镶边框的矩形镜子，要求宽与长之比为1：2．售货员介绍镜子价格计算公式为：镜子总价（元）=镜面面积（平方米）×单价（a元/平方米）+边框长度（米）×单价（b元/米）+加工费（20元/块）．（边框宽度忽略不计）
（1）写出镜子的总价y（元）与矩形镜面宽x（米）之间的关系式（用含a、b的式子表示，不要求写出自变量取值范围）．
（2）售货员为小王计算了两种规格镜子的价格：①宽0.5米×长1米，总价为110元；②宽1米×长2米，总价为320元，请求出a和b的值．
（3）小王花了200元买回一块镜子，请你求出他购买的镜子的规格．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网