Question

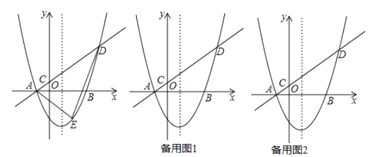
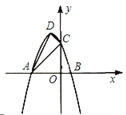
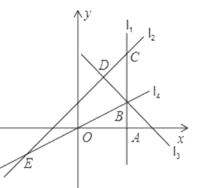
【题目】如图，直线 轴于点 ，点是直线 上的动点．直线 交 于点 ，过点 作直线 垂直于 ，垂足为 ，过点 ， 的直线 交 于点 E，当直线 ，，能围成三角形时，设该三角形面积为 ，当直线 ，，能围成三角形时，设该三角形面积为 ．

（1）若点 在线段 上，且 ，则 点坐标为_________；

（2）若点 在直线上，且，则的度数为_______.

Answer 1

【答案】 或

【解析】

（1）设B的坐标是（2，m），则△BCD是等腰直角三角形，即可表示出S1，求得直线l1的解析式，解方程组即可求得E的坐标，则S2的值即可求得，根据S1=S2，即可得到一个关于m的方程从而求得m的值；
（2）分类讨论，根据S2=S1，即可得到一个关于m的方程从而求得m的值，根据勾股定理，求得角的度数．

解：（1）设B的坐标是（2，m），
∵直线l2：y=x+1交l1于点C，
∴∠ACE=45°，
∴△BCD是等腰直角三角形．
BC=|3-m|，
则BD=CD=BC=|3-m|，

S1=×（|3-m|）2=（3-m）2．
设直线l4的解析式是y=kx，过点B，
则2k=m，解得：k=，
则直线l4的解析式是y=x．
根据题意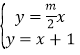得： ，解得：，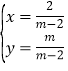
则E的坐标是（，）．
S△BCE=BC|2|=|3-m|||=．
∴S2=S△BCE-S1=- （3-m）2 ．
当S1=S2时，-（3-m）2=（3-m）2．
解得：m1=4或m2=0，
易得点C坐标为（2，3），即AC=3，
∵点B在线段AC上，
∴m1=4不合题意舍去，
则B的坐标是（2，0）；
（2）分三种情况：
①当点B在线段AC上时
当S2=S1时，-（3-m）2= （3-m）2．
解得：m=4-2 或2（不在线段AC上，舍去），或m=3（l2和l4重合，舍去）．
则AB=4-2．
在OA上取点F，使OF=BF，连接BF，设OF=BF=x．

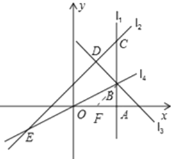
则AF=2-x，根据勾股定理，x2＝(2x)2+(42)2，
解得：x＝84，
∴sin∠BFA=＝，
∴∠BFA=30°，
∴∠BOA=15°；
或由s1=s2可得CD=DE，所以BD是CE的中垂线，所以BC=BE，根据∠BCD=45°即可知CB⊥BO，所以B必须与A重合，所以B（2，0），
②当点B在AC延长线上时，

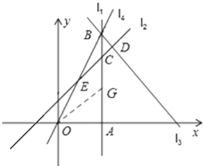
此时，S2＝S△BCE+S1＝+ (3m)2
当S2=S1时，得：+(3m)2＝

(3m)2，
解得符合题意有：AB=4+2．
在AB上取点G，使BG=OG，连接OG，设BG=OG=x，
则AG=4+2-x．根据勾股定理，得x2＝(4+2x)2+22，
解得：x=4，
∴sin∠OGA=＝，
∴∠OGA=30°，
∴∠OBA=15°，
∴∠BOA=75°；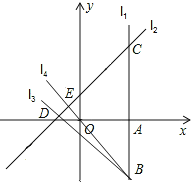

③当点B在CA延长线上时，S1＞S2，
此时满足条件的点B不存在，
综上所述，∠BOA的度数为15°或75°．