题目内容
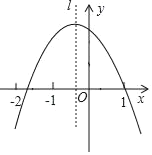
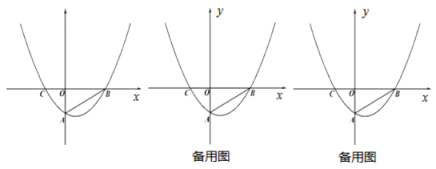
【题目】如图,平面直角坐标系中,抛物线![]() 与
与![]() 轴交于B、C两点(点B在点C右侧),与
轴交于B、C两点(点B在点C右侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)求抛物线的解析式;
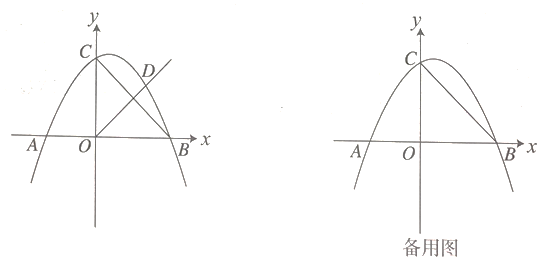
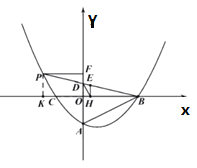
(2)点P在第二象限的抛物线上,连接PB交![]() 轴于D,取PB的中点E,过点E作
轴于D,取PB的中点E,过点E作![]() 轴于点H,连接DH,设点P的横坐标为
轴于点H,连接DH,设点P的横坐标为![]() .
.![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式(不要求写出自变量
的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
(3)在(2)的条件下,作![]() 轴于F,连接CP、CD,
轴于F,连接CP、CD,![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() 交
交![]() 轴于点
轴于点![]() ,连接BF并延长交抛物线于点
,连接BF并延长交抛物线于点![]() .
.![]() ,在射线CS上取点Q.连接QF,
,在射线CS上取点Q.连接QF,![]() ,求直线
,求直线![]() 的解析式.
的解析式.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)先把![]() 、
、![]() 两点坐标求解出来,再根据待定系数法即可把函数解析式求解出来;
两点坐标求解出来,再根据待定系数法即可把函数解析式求解出来;
(2) 过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,把OH、OD的长度用t表示出来,再根据
,把OH、OD的长度用t表示出来,再根据![]() 的面积为
的面积为![]() ,即可表示出
,即可表示出![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)先证明![]() ,再过点R作
,再过点R作![]() 轴,设
轴,设![]() ,连接
,连接![]() 、
、![]() ,作
,作![]() 于
于![]() ,求出Q点的坐标,再利用待定系数法即可把直线
,求出Q点的坐标,再利用待定系数法即可把直线![]() 的解析式求解出来;
的解析式求解出来;
(1)∵![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点
两点
∴令![]() ,即
,即![]()
解得![]() ,
,![]()
由题意得,∴![]() ,
,![]()
在![]() 中,
中,![]() ,
,![]() .
.
∴![]()
∴![]()
∴![]()
∴![]()
∴抛物线的解析式为![]()
(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]()
∴![]() ,
,![]()
∴四边形![]() 为矩形
为矩形
∴![]()
∵![]() 为
为![]() 的中点
的中点
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
∵![]()
∴![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∵![]() ,
,
即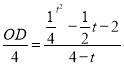
∴![]()
∴![]() ,
,
(3)∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]()
过点R作![]() 轴,如图
轴,如图
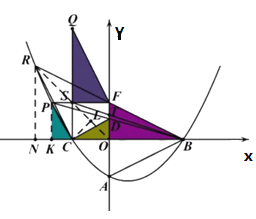
设![]()
∴![]() ,
,
∴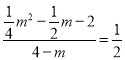
解得![]() 或
或![]() (舍去),
(舍去),
∴![]()
∴![]()
∴![]()
连接![]() 、
、![]() ,作
,作![]() 于
于![]() ,如上图
,如上图
∵![]()
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
∵![]() ,
,
∴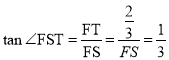
∴![]() ,
,
∴![]() ,
,
∴![]()
∵![]() ,
,![]() ,
,
∴![]()
∴![]()
∴![]()
设直线![]() 的解析式为
的解析式为![]()
∴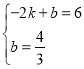 解得
解得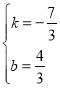
∴直线![]() 的解析式为
的解析式为![]() .
.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】观察下表:
序号 | 1 | 2 | 3 | … |
图形 |
|
|
| … |
我们把某格中字母和所得到的多项式称为特征多项式,例如:
第1格的“特征多项式”为![]() ;
;
第2格的“特征多项式”为![]() .
.
回答下列问题:
(1)第3格的“特征多项式”为________________,
第4格的“特征多项式”为______________________,
第![]() 格的“特征多项式”为___________________;
格的“特征多项式”为___________________;
(2)若第1格的“特征多项式”的值为![]() ,第2格的“特征多项式”的值为
,第2格的“特征多项式”的值为![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,第![]() 格的特征多项式的值为
格的特征多项式的值为![]() ,则直接写出
,则直接写出![]() 的值;若没有,请说明理由.
的值;若没有,请说明理由.