题目内容
 如图,已知∠AOB=30°,P为∠AOB内一点,OP=10cm,分别作出P关于OA、OB的对称点P1、P2,连接P1P2交OA、OB于M、N,则△MNP的周长为
如图,已知∠AOB=30°,P为∠AOB内一点,OP=10cm,分别作出P关于OA、OB的对称点P1、P2,连接P1P2交OA、OB于M、N,则△MNP的周长为10
10
cm.分析:根据轴对称的性质可得∠P1OA=∠AOP,∠P2OB=∠BOP,PM=P1M,PN=P2N,P1O=PO=P2O,从而求出△OP1P2是等边三角形,△MNP的周长等于P1P2,从而得解.
解答:解:∵P1、P2分别是P关于OA、OB的对称点,
∴∠P1OA=∠AOP,∠P2OB=∠BOP,PM=P1M,PN=P2N,P1O=PO=P2O,
∴∠P1OP2=∠P1OA+∠AOP+∠P2OB+∠BOP=2∠AOB,
∵∠AOB=30°,
∴∠P1OP2=2×30°=60°,
∴△OP1P2是等边三角形,
又∵△MNP的周长=PM+MN=PN=P1M+MN+P2N=P1P2,
∴△MNP的周长=P1P2=P1O=PO=10cm.
故答案为:10.
∴∠P1OA=∠AOP,∠P2OB=∠BOP,PM=P1M,PN=P2N,P1O=PO=P2O,
∴∠P1OP2=∠P1OA+∠AOP+∠P2OB+∠BOP=2∠AOB,
∵∠AOB=30°,
∴∠P1OP2=2×30°=60°,
∴△OP1P2是等边三角形,
又∵△MNP的周长=PM+MN=PN=P1M+MN+P2N=P1P2,
∴△MNP的周长=P1P2=P1O=PO=10cm.
故答案为:10.
点评:本题考查了轴对称的性质,等边三角形的判定与性质,熟记性质得到相等的边与角是解题的关键.

练习册系列答案
相关题目
如图,已知∠AOB是直角,∠AOC是锐角,ON平分∠AOC,OM平分∠BOC,则∠MON是( )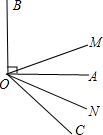

| A、45° | ||
B、45°+
| ||
C、60°-
| ||
| D、不能计算 |


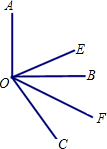 如图,已知∠AOB是直角,∠BOC=60°,OE平分∠AOC,OF平分∠BOC.
如图,已知∠AOB是直角,∠BOC=60°,OE平分∠AOC,OF平分∠BOC. 尺规作图:
尺规作图: 如图,已知∠AOB=x(0°<x<180°),OC平分∠AOB,点N为OB上一个定点.通过画图可以知道:当∠AOB=45°时,在射线OC上存在点P,使△ONP成为等腰三角形,且符合条件的点有三个,即P1(顶点为P2),P2(顶点为0),P3(顶点为N).
如图,已知∠AOB=x(0°<x<180°),OC平分∠AOB,点N为OB上一个定点.通过画图可以知道:当∠AOB=45°时,在射线OC上存在点P,使△ONP成为等腰三角形,且符合条件的点有三个,即P1(顶点为P2),P2(顶点为0),P3(顶点为N).