Question

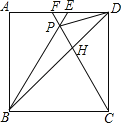
【题目】在平面直角坐标系xOy中，抛物线y＝x2+bx+c交x轴于A（﹣1，0），B（3，0）两点，交y轴于点C．

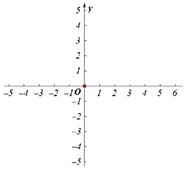
（1）如图1，求抛物线的解析式；

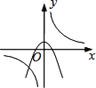
（2）如图2，点P是第一象限抛物线上的一个动点，连接CP交x轴于点E，过点P作PK∥x轴交抛物线于点K，交y轴于点N，连接AN、EN、AC，设点P的横坐标为t，四边形ACEN的面积为S，求S与t之间的函数关系式（不要求写出自变量t的取值范围）；

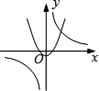
（3）如图3，在（2）的条件下，点F是PC中点，过点K作PC的垂线与过点F平行于x轴的直线交于点H，KH＝CP，点Q为第一象限内直线KP下方抛物线上一点，连接KQ交y轴于点G，点M是KP上一点，连接MF、KF，若∠MFK＝∠PKQ，MP＝AE+GN，求点Q坐标．

Answer 1

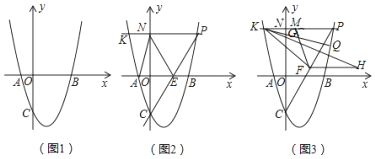
【答案】（1）y＝x2﹣2x﹣3；（2）S＝t2+t；（3）Q（，）．

【解析】

（1）函数的表达式为：y＝（x+1）（x﹣3），即可求解；

（2）tan∠PCH＝＝＝，求出OE＝，利用S＝S△NCE+S△NAC，即可求解；

（3）证明△CNP≌△KRH，求出点P（4，5）确定tan∠QKP＝＝＝4﹣m＝tan∠QPK＝＝NG，最后计算KT＝MT＝（），FT＝4﹣（+），tan∠MFT＝＝4﹣m，即可求解．

（1）函数的表达式为：y＝（x+1）（x﹣3）＝x2﹣2x﹣3；

（2）过点P作PH⊥y轴交于点H，设点P（t，t2﹣2t﹣3），

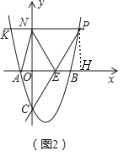
CN＝t2﹣2t﹣3+3＝t2﹣2t，

∴tan∠PCH＝＝＝，

，解得：OE＝，

S＝S△NCE+S△NAC＝AE×CN＝t2+t；

（3）过点K作KR⊥FH于点R，

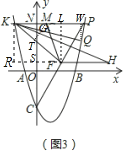
∵KH＝CP，∠NCP＝∠H，∠R＝∠PNC＝90°，

∴△CNP≌△KRH，∴PN＝KR＝NS，

∵点F是PC中点，SF∥NP，

∴PN＝KR＝NS＝CN，即t＝（t2﹣2t﹣3+3），

解得：t＝0或4（舍去0），点P（4，5），

点K、P时关于对称轴的对称点，故点K（﹣2，5），

∵OE∥PN，则，故OE＝，同理AE＝，

设点Q（m，m2﹣2m﹣3），过点Q作WQ⊥KP于点W，

WQ＝5﹣（m2﹣2m﹣3）＝﹣m2+2m+8，WK＝m+2，

tan∠QKP＝＝＝4﹣m＝tan∠QPK＝＝NG，

则NG＝8﹣2m，

MP＝AE+GN＝（8﹣2m）＝﹣m+，

KM＝KP﹣MP＝，

过点F作FL⊥KP于点L，点F（2，1），

则FL＝LK＝4，则∠LKF＝45°，

∵∠MFK＝∠PKQ，

tan∠MFK＝tan∠QKP＝4﹣m，

过点M作MT⊥FK于点T，则KT＝MT＝（），

FT＝4﹣（），

tan∠MFT＝＝4﹣m，

解得：m＝11或（舍去11），

故点Q（，）．