题目内容
甲乙两名同学做摸球游戏,他们把三个分别标有1,2,3的大小和形状完全相同的小球放在一个不透明的口袋中.
(1)求从袋中随机摸出一球,标号是1的概率;
(2)从袋中随机摸出一球后放回,摇匀后再随机摸出一球,若两次摸出的球的标号之和为偶数时,则甲胜;若两次摸出的球的标号之和为奇数时,则乙胜;试分析这个游戏是否公平?请说明理由.


解:(1)∵三个分别标有1,2,3的大小和形状完全相同的小球放在一个不透明的口袋中,
∴从袋中随机摸出一球,标号是1的概率为: ;
;
(2)这个游戏不公平.
画树状图得:

∵共有9种等可能的结果,两次摸出的球的标号之和为偶数的有5种情况,两次摸出的球的标号之和为奇数的有4种情况,
∴P(甲胜)= ,P(乙胜)=
,P(乙胜)= .
.
∴P(甲胜)≠P(乙胜),
∴这个游戏不公平.


练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
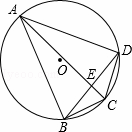
如图,点A,B,C,D都在⊙O上,AC,BD相交于点E,则∠ABD=( )
|
| A. | ∠ACD | B. | ∠ADB | C. | ∠AED | D. | ∠ACB |



 在同一坐标系中的图象大致是( )
在同一坐标系中的图象大致是( )





 D.
D. 

 (x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
(x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
 B.
B.  C.
C.  D.
D. 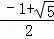
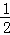 ,求EM:MF的值.
,求EM:MF的值.